题目内容
已知双曲线
-
=1的左右顶点分别为A1A2,点P是双曲线上任一点,Q是P关于x轴的对称点,求直线A1P与A2Q交点M的轨迹E的方程.
| x2 |
| 9 |
| y2 |
| 16 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设点p(x0,y0),为A1(-3,0),A2(3,0),直线A1P方程是y=
(x+3),①;线A2Q的方程是y=
(x-3),②;
-
=1,③
3个方程联合化简即可得出直线A1P与A2Q交点M的轨迹E的方程.
| y0 |
| x+3 |
| -y0 |
| x0-3 |
| ||
| 9 |
| ||
| 16 |
3个方程联合化简即可得出直线A1P与A2Q交点M的轨迹E的方程.
解答:
解:双曲线的左右顶点分别为A1(-3,0),A2(3,0),点p(x0,y0),
设M关于x轴对称点为Q(x0,-y0)
直线A1P方程是y=
(x+3),①
线A2Q的方程是y=
(x-3),②
-
=1,③
①×②得;y2=
(x2-9)④
即x
=9(
+1)⑤
把⑤代入③方程化简得交点P的轨迹E的方程:
+
=1,(x≠0,y≠0)
设M关于x轴对称点为Q(x0,-y0)
直线A1P方程是y=
| y0 |
| x+3 |
线A2Q的方程是y=
| -y0 |
| x0-3 |
| ||
| 9 |
| ||
| 16 |
①×②得;y2=
| -y02 | ||
|
即x
2 0 |
| y02 |
| 16 |
把⑤代入③方程化简得交点P的轨迹E的方程:
| x2 |
| 9 |
| y2 |
| 16 |
点评:本题综合考察了直线,双曲线的方程,直线与圆锥曲线的位置关系,联合化简得出轨迹方程,运算仔细.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数中,周期为π,且在[0,
]上为减函数的是( )
| π |
| 2 |
A、y=sin(2x+
| ||
B、y=cos(2x+
| ||
C、y=sin(x+
| ||
D、y=cos(x+
|
三名男生和三名女生站成一排,若男生甲不站在两端,任意两名女生都不相邻,则不同的排列种数是( )
| A、120 | B、96 | C、84 | D、36 |
函数f(x)=x3+3x-1在以下哪个区间一定有零点( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
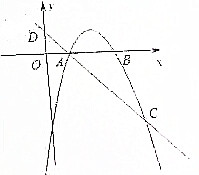 如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).