命题“存在x∈R，使x2+ax-4a＜0，为假命题”是命题“-16≤a≤0”的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
已知平面向量
，
（α≠0，α≠β）满足|
|=1，且
与
-
的夹角为120°，则|
|的取值范围是（ ）
| α |
| β |
| β |
| α |
| β |
| α |
| α |
A、[0，
| ||||
B、[0，
| ||||
C、(0，
| ||||
D、(
|
甲，乙两位同学考入某大学的同一专业，已知该专业设有3个班级，则他们被随机分到同一个班级的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如果
＜θ＜
，那么下列各式中正确的是（ ）
| π |
| 4 |
| π |
| 2 |
| A、cosθ＜tanθ＜sinθ |
| B、sinθ＜cosθ＜tanθ |
| C、tanθ＜sinθ＜cosθ |
| D、cosθ＜sinθ＜tanθ |
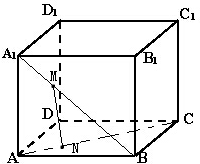已知正方体ABCD-A1B1C1D1的棱长为a，M、N分别为A1B和AC上的点，A1M=AN=已知tan（α+β）=
，tan（α-
)=
=
，那么tan（β+
）=（ ）
| 2 |
| 5 |
| π |
| 6 |
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|