题目内容
甲，乙两位同学考入某大学的同一专业，已知该专业设有3个班级，则他们被随机分到同一个班级的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：由古典概型概率公式求解．
解答：
解：甲，乙两位同学考入某大学的同一专业，则他们被随机分班的情况有3×3=9种
甲，乙两位同学考入同一班级的情况有3种
故概率为
=
．
故选C．
甲，乙两位同学考入同一班级的情况有3种
故概率为
| 3 |
| 9 |
| 1 |
| 3 |
故选C．
点评：本题考查等可能事件的概率，考查利用排列组合解决实际问题，考查学生的计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知平面向量
，
（
≠0，
≠
）满足|
|=1，且
与
-
的夹角为30°，则|
|的取值范围是（ ）
| α |
| β |
| α |
| α |
| β |
| β |
| α |
| α |
| β |
| α |
A、(0，
| ||||
| B、（0，2] | ||||
C、(1，
| ||||
| D、（1，2] |
函数f（x）=lnx-1的零点所在的区间是（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
已知tan（α+β）=
，tan（α-
)=
=
，那么tan（β+
）=（ ）
| 2 |
| 5 |
| π |
| 6 |
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
过正三棱锥一侧棱及其外接球的球心O所作截面如图所示，则这个正三棱锥的侧面三角形的顶角为（ ）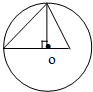
| A、60° | ||
| B、90° | ||
| C、120° | ||
D、arccos
|