题目内容
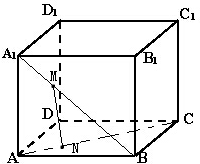已知正方体ABCD-A1B1C1D1的棱长为a，M、N分别为A1B和AC上的点，A1M=AN=
| ||
| 3 |
（1）求证：MN∥面BB1C1C；
（2）求MN的长．
考点：直线与平面平行的判定,点、线、面间的距离计算
专题：空间位置关系与距离
分析：（1）由于CD⊥平面B1BCC1，所以
是平面B1BCC1的法向量，因此只需证明向量
•
=0，建立空间直角坐标系，得到所需向量的坐标，通过数量积证明MN所在的向量与面BB1C1C的法向量垂直；
（2）由（1）得到
的坐标，通过求其模求MN 的长度．
| DC |
| MN |
| DC |
（2）由（1）得到
| MN |
解答：
证明：∵正方体棱长为a，建立D-xyz坐标系，如图，
因为A1M=AN=
a，
∴M（a，
a，
a），N（
a，
a，0），所以
=（-
a，0，-
a），
又∵
=（0，a，0）是平面B1BCC1的法向量，
且
•
=0，
∴
⊥
，
∴MN∥平面B1BCC1．
（2）∵
=（-
a，0，-
a），
∴MN=
=
a．
因为A1M=AN=
| ||
| 3 |
∴M（a，
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| MN |
| 1 |
| 3 |
| 2 |
| 3 |
又∵
| DC |
且
| MN |
| DC |
∴
| MN |
| DC |
∴MN∥平面B1BCC1．
（2）∵
| MN |
| 1 |
| 3 |
| 2 |
| 3 |
∴MN=
(-
|
| ||
| 3 |
点评：本题考查线面平行的判定以及线段长度，在正方体为载体的几何证明中，通常建立空间直角坐标系，通过向量的运算证明线面关系等．
练习册系列答案
相关题目