题目内容
命题“存在x∈R,使x2+ax-4a<0,为假命题”是命题“-16≤a≤0”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:求出命题的等价条件,利用充分条件和必要条件的定义即可得到结论.
解答:
解:若“存在x∈R,使x2+ax-4a<0为假命题,
即“任意x∈R,使x2+ax-4a≥0为真命题,即判别式△=a2+16a≤0,
解得-16≤a≤0,
∵-16≤a≤0是-16<a<0的必要不充分条件,
故选:B.
即“任意x∈R,使x2+ax-4a≥0为真命题,即判别式△=a2+16a≤0,
解得-16≤a≤0,
∵-16≤a≤0是-16<a<0的必要不充分条件,
故选:B.
点评:本题主要考查充分条件和必要条件的判断,求出命题的等价条件是解决本题的关键.

练习册系列答案
相关题目
设点O是△ABC的外心,AB=13,AC=12,则
•
为( )
| BC |
| AO |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如果
<θ<
,那么下列各式中正确的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosθ<tanθ<sinθ |
| B、sinθ<cosθ<tanθ |
| C、tanθ<sinθ<cosθ |
| D、cosθ<sinθ<tanθ |
已知θ是三角形的一个内角,且sinθ+cosθ=
,则x2sinθ-y2cosθ=1表示( )
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在x轴上的双曲线 |
| C、焦点在y轴上的椭圆 |
| D、焦点在y轴上的双曲线 |
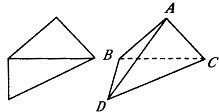 如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.
如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.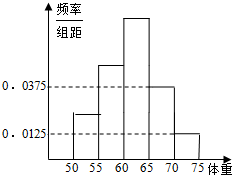 为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )
为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )