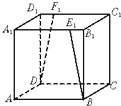
 如图,正方体ABCD-A1B1C1D1中,E1、F1分别是A1B1、C1D1上的点,并且4B1E1=4D1F1=A1B1,则BE1与DF1所成角的余弦值是( )
如图,正方体ABCD-A1B1C1D1中,E1、F1分别是A1B1、C1D1上的点,并且4B1E1=4D1F1=A1B1,则BE1与DF1所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若正n边形的两条对角线都与直线l垂直,则直线l一定垂直于这个正n边形所在的平面,则n的取值可能是( )
| A、8 | B、7 | C、6 | D、5 |
已知sinα+cosα=
,则sinα•cosα的值为( )
| 17 |
| 13 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
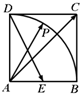 如图在边长为2的正方形ABCD中,E为边AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量
如图在边长为2的正方形ABCD中,E为边AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量