Question

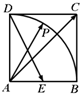如图在边长为2的正方形ABCD中，E为边AB的中点，P为以A为圆心、AB为半径的圆弧上的任意一点，设向量

AP

=x

DE

+y

AC

，则x+y的最小值为

 

．

Answer 1

考点：平面向量的基本定理及其意义

专题：平面向量及应用

分析：建立坐标系，由正方形ABCD的边长为2，求出向量

AP

=x

DE

+y

AC

=x（1，-2）+y（2，2）=（x+2y，-2x+2y）=（2cosθ，2sinθ），用cosθ，sinθ表示x和y，根据cosθ，sinθ 的取值范围，再结合x+y的单调性，求出x+y的最小值．

解答： 解：以A为原点，以AB所在的为x轴，建立坐标系，由正方形ABCD的边长为2，
则E（1，0），C（2，2），D（0，2），A（0，0）．   
设 P（2cosθ，2sinθ），0≤θ≤

π

2

，
∴

AC

=（2，2）． 
再由向量

AP

=x

DE

+y

AC

=x（1，-2）+y（2，2）=（x+2y，-2x+2y）=（2cosθ，2sinθ），
∴

x+2y=2cosθ -2x+2y=2sinθ

，
解得：

x= 2 3 (cosθ-sinθ) y= 1 3 (2cosθ+sinθ)

∴x+y=

2

3

•2cosθ-

1

6

•2sinθ=

4

3

cosθ-

1

3

sinθ．
由题意得 0≤θ≤

π

2

，
∴0≤cosθ≤1，0≤sinθ≤1．
求得（x+y）′=-

4

3

sinθ-

1

3

cosθ＜0，
故x+y在[0，

π

2

]上是减函数，故当θ=

π

2

时，即cosθ=0，这时x+y取最小值为-

1

3

，
故答案为：-

1

3

．

点评：本题考查两个向量坐标形式的运算，根据cosθ，sinθ 的取值范围求三角函数式的最值，利用导数研究函数的单调性．用cosθ，sinθ表示x和y是解题的难点，属于中档题．