题目内容
已知方程8x2+6kx+2k+1=0的两个实根是sinθ和cosθ.
(1)求k的值;
(2)求tanθ的值(其中sinθ>cosθ).
(1)求k的值;
(2)求tanθ的值(其中sinθ>cosθ).
考点:同角三角函数基本关系的运用
专题:函数的性质及应用,三角函数的求值
分析:(1)由题意,利用韦达定理得到sinθ+cosθ=-
,sinθcosθ=
,根据sin2θ+cos2θ=1列出关于k的方程,求出方程的解即可得到k的值;
(2)将k值代入可得sinθ+cosθ的值和sinθcosθ的值,由sinθ>cosθ,可求sinθ-cosθ的值,从而可求tanθ的值.
| 3k |
| 4 |
| 2k+1 |
| 8 |
(2)将k值代入可得sinθ+cosθ的值和sinθcosθ的值,由sinθ>cosθ,可求sinθ-cosθ的值,从而可求tanθ的值.
解答:
解:(1)∵sinθ,cosθ是关于x的方程8x2+6kx+2k+1=0的两个实根,
∴sinθ+cosθ=-
,sinθcosθ=
,
∵sin2θ+cos2θ=1,
∴(sinθ+cosθ)2-2sinθcosθ=1,即
-
=1,
整理得:(k-2)(9k+10)=0,
解得:k=2或k=-
,
由于k=2时△<0故舍去.故k=-
.
(2)由(1)知,把k=-
代入,得sinθ+cosθ=
,sinθcosθ=-
,
∵sinθ>cosθ,
sinθ-cosθ=
=
=
,
∴sinθ=
,cosθ=
,
∴tanθ=
=
=-
=-
.
∴sinθ+cosθ=-
| 3k |
| 4 |
| 2k+1 |
| 8 |
∵sin2θ+cos2θ=1,
∴(sinθ+cosθ)2-2sinθcosθ=1,即
| 9k2 |
| 16 |
| 2k+1 |
| 4 |
整理得:(k-2)(9k+10)=0,
解得:k=2或k=-
| 10 |
| 9 |
由于k=2时△<0故舍去.故k=-
| 10 |
| 9 |
(2)由(1)知,把k=-
| 10 |
| 9 |
| 5 |
| 6 |
| 11 |
| 72 |
∵sinθ>cosθ,
sinθ-cosθ=
| 1-2sinθcosθ |
1+2×
|
| ||
| 6 |
∴sinθ=
| ||
| 12 |
5-
| ||
| 12 |
∴tanθ=
| sinθ |
| cosθ |
| ||
5-
|
72+10
| ||
| 22 |
36+5
| ||
| 11 |
点评:此题考查了同角三角函数间基本关系的运用,考察了韦达定理的应用,熟练掌握基本关系是解本题的关键,属于基本知识的考查.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),若直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,则实数k的取值范围为( )
A、(2
| ||||||
B、(
| ||||||
C、(2
| ||||||
| D、(4,8) |
一个几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的外接球体积为( )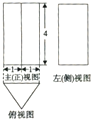

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
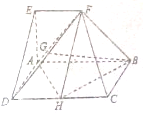 如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD
如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD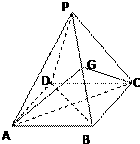 如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2,G是PB的中点.
如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2,G是PB的中点.