题目内容
已知x,y∈R+,且2x+8y-xy=0,当x,y为何值时,x+y取得最小值,并求出最小值.
考点:基本不等式
专题:不等式的解法及应用
分析:根据条件得出
+
=1,变形∴x+y=(x+y)(
+
)=10+
+
,运用基本不等式求解即可.
| 2 |
| y |
| 8 |
| x |
| 2 |
| y |
| 8 |
| x |
| 8y |
| x |
| 2x |
| y |
解答:
解:∵x,y∈R+,且2x+8y-xy=0,
∴
+
=1,
∴x+y=(x+y)(
+
)=10+
+
≥10+2
=10+2×4=18,
当且仅当
=
,x=2y,
∵
+
=1,
∴y=6,x=12,
∴当y=6,x=12时,x+y取得最小值18.
∴
| 2 |
| y |
| 8 |
| x |
∴x+y=(x+y)(
| 2 |
| y |
| 8 |
| x |
| 8y |
| x |
| 2x |
| y |
| 2×8 |
当且仅当
| 8y |
| x |
| 2x |
| y |
∵
| 2 |
| y |
| 8 |
| x |
∴y=6,x=12,
∴当y=6,x=12时,x+y取得最小值18.
点评:本题本考查了代数式的变形,基本不等式的运用,属于中档题.

练习册系列答案
相关题目
若正n边形的两条对角线都与直线l垂直,则直线l一定垂直于这个正n边形所在的平面,则n的取值可能是( )
| A、8 | B、7 | C、6 | D、5 |
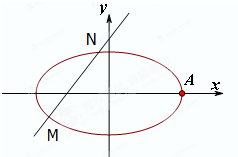 如图,已知点A是椭圆
如图,已知点A是椭圆
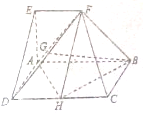 如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD
如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD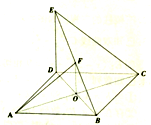 如图,菱形ABCD的边长为2,对角线交于点O,DE⊥平面ABCD;
如图,菱形ABCD的边长为2,对角线交于点O,DE⊥平面ABCD;