设椭圆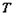 :
: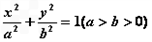 ,直线
,直线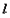 过椭圆左焦点
过椭圆左焦点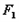 且不与
且不与 轴重合,
轴重合,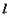 与椭圆交于
与椭圆交于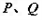 ,当
,当 与
与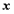 轴垂直时,
轴垂直时,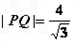 ,
,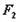 为椭圆的右焦点,
为椭圆的右焦点,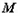 为椭圆
为椭圆 上任意一点,若
上任意一点,若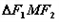 面积的最大值为
面积的最大值为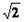 .
.
(1)求椭圆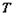 的方程;
的方程;
(2)直线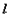 绕着
绕着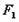 旋转,与圆
旋转,与圆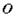 :
: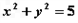 交于
交于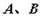 两点,若
两点,若 ,求
,求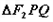 的面积
的面积 的取值范围.
的取值范围.
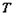 :
: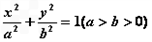 ,直线
,直线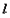 过椭圆左焦点
过椭圆左焦点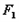 且不与
且不与 轴重合,
轴重合,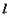 与椭圆交于
与椭圆交于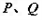 ,当
,当 与
与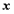 轴垂直时,
轴垂直时,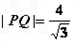 ,
,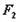 为椭圆的右焦点,
为椭圆的右焦点,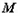 为椭圆
为椭圆 上任意一点,若
上任意一点,若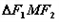 面积的最大值为
面积的最大值为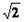 .
.(1)求椭圆
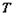 的方程;
的方程;(2)直线
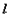 绕着
绕着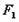 旋转,与圆
旋转,与圆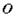 :
: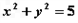 交于
交于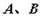 两点,若
两点,若 ,求
,求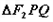 的面积
的面积 的取值范围.
的取值范围. 在R上是单调函数,则实数a的取值范围是( )。
在R上是单调函数,则实数a的取值范围是( )。 ,曲线
,曲线 在
在 处的切线方程为
处的切线方程为 。
。 的单调区间;
的单调区间;
 ,
, ,其中min{f(x)|x∈D}表示函数f(x)在D上的最小值,max{f(x)|x∈D}表示函数f(x)在D上的最大值,若存在最小正整数k,使得f2(x)-f1(x)≤k(x-a),对任意的x∈[a,b]成立,则称函数f(x)为[a,b]上的“k阶收缩函数”.
,其中min{f(x)|x∈D}表示函数f(x)在D上的最小值,max{f(x)|x∈D}表示函数f(x)在D上的最大值,若存在最小正整数k,使得f2(x)-f1(x)≤k(x-a),对任意的x∈[a,b]成立,则称函数f(x)为[a,b]上的“k阶收缩函数”. ,函数f(x)=-x3+3x2是[0,b]上的2阶收缩函数,求b的取值范围
,函数f(x)=-x3+3x2是[0,b]上的2阶收缩函数,求b的取值范围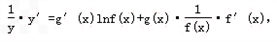 于是得到:
于是得到: 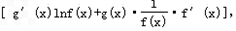 运用此方法求得函数
运用此方法求得函数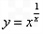 的一个单调递增区间是
的一个单调递增区间是 x3-2x2+bx+a,g(x)=ln(1+2x)+x
x3-2x2+bx+a,g(x)=ln(1+2x)+x <x1<t<x2, 求证:割线AC 的斜率大于割线BC 的斜率;
<x1<t<x2, 求证:割线AC 的斜率大于割线BC 的斜率;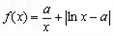 ,
,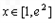 .
.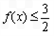 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.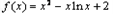 ,
,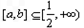 ,使f(x)在[a,b]上的值域是
,使f(x)在[a,b]上的值域是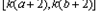 ,求k的取值范围.
,求k的取值范围. 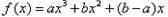 (
(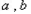 不同时为零的常数),导函数为
不同时为零的常数),导函数为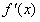
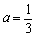 时,若存在
时,若存在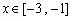 ,使得
,使得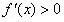 成立,求
成立,求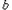 的取值范围;
的取值范围;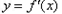 在
在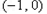 内至少有一个零点;
内至少有一个零点; 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线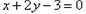 ,关于
,关于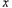 的方程
的方程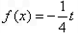 在
在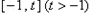 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围.