题目内容
已知a>0,函数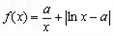 ,
,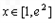 .
.
(Ⅰ)当a=3时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(Ⅱ)若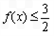 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
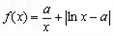 ,
,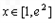 .
.(Ⅰ)当a=3时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(Ⅱ)若
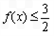 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.解:(Ⅰ)当a=3时,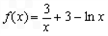
∴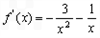 ,
,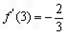 ,
,
又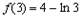 ,
,
∴曲线y=f(x)在点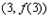 处的切线方程为:
处的切线方程为: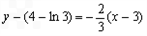 ,
,
即: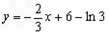 .
.
(Ⅱ)由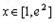 得
得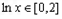
①当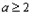 时
时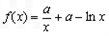 ,
,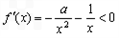 ,
,
∴f(x)在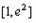 上递减,
上递减,
∴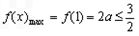 ,∴
,∴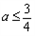 ,此时a不存在;
,此时a不存在;
②当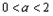 时若
时若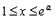 时,
时,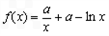
由①得f(x)在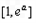 上递减,
上递减,
∴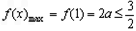 ∴
∴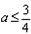 ,此时
,此时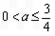
若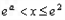 时
时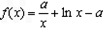 ,∴
,∴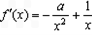
令f′(x)=0得x=a,
又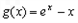 在(0,2)递增,
在(0,2)递增,
故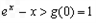 ∴
∴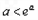 ,
,
当
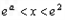 时
时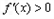 ,∴f(x)在
,∴f(x)在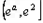 递增,
递增,
∴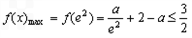
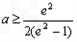 ,
,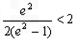 ,∴
,∴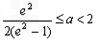 ,
,
又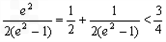 ,∴
,∴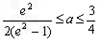
综上知,实数a的取值范围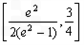
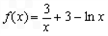
∴
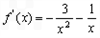 ,
,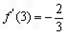 ,
,又
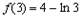 ,
,∴曲线y=f(x)在点
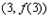 处的切线方程为:
处的切线方程为: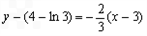 ,
,即:
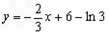 .
.(Ⅱ)由
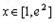 得
得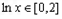
①当
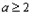 时
时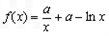 ,
,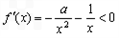 ,
,∴f(x)在
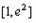 上递减,
上递减,∴
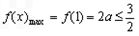 ,∴
,∴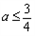 ,此时a不存在;
,此时a不存在;②当
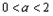 时若
时若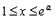 时,
时,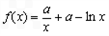
由①得f(x)在
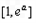 上递减,
上递减,∴
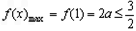 ∴
∴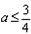 ,此时
,此时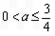
若
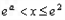 时
时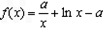 ,∴
,∴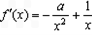
令f′(x)=0得x=a,
又
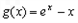 在(0,2)递增,
在(0,2)递增,故
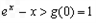 ∴
∴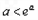 ,
,当

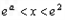 时
时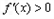 ,∴f(x)在
,∴f(x)在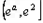 递增,
递增,∴
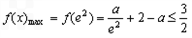
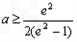 ,
,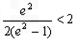 ,∴
,∴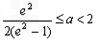 ,
, 又
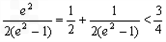 ,∴
,∴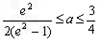
综上知,实数a的取值范围
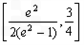

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A、?x∈R,f(x)≤f(x0) | B、?x∈R,f(x)≥f(x0) | C、?x∈R,f(x)≤f(x0) | D、?x∈R,f(x)≥f(x0) |
已知a>0,函数f(x)=(x2-2ax)ex的最小值所在区间是( )
A、(-∞,a-1-
| ||
B、(a-1-
| ||
| C、(0,2a) | ||
| D、(2a,+∞) |