题目内容
设函数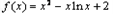 ,
,
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在区间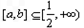 ,使f(x)在[a,b]上的值域是
,使f(x)在[a,b]上的值域是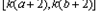 ,求k的取值范围.
,求k的取值范围.
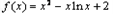 ,
,(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在区间
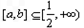 ,使f(x)在[a,b]上的值域是
,使f(x)在[a,b]上的值域是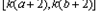 ,求k的取值范围.
,求k的取值范围. 解:(Ⅰ)令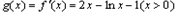 ,则
,则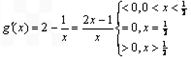 ,
,
所以g(x)在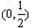 单调递减,在
单调递减,在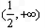 单调递增,
单调递增,
则g(x)的最小值为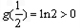 .
.
所以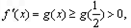 所以f(x)的单调递增区间是(0,+∞)
所以f(x)的单调递增区间是(0,+∞)
【另解】 ∵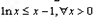 ,∴
,∴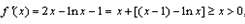
所以f(x)的单调递增区间是(0,+∞)
(Ⅱ)由(Ⅰ)得f(x)在区间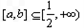 递增,
递增,
∵f(x)在[a,b]上的值域是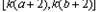
所以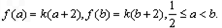
则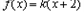 在
在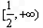 上至少有两个不同的正根,
上至少有两个不同的正根,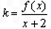 ,
,
令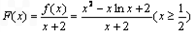 求导,得
求导,得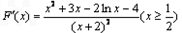 ,
,
令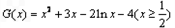 则
则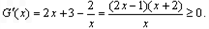
所以G(x)在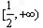 递增,
递增,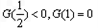 .
.
当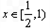 时,
时,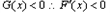 ,
,
当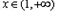 时,
时,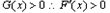
所以F(x)在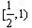 上递减,在(1,+∞)上递增,
上递减,在(1,+∞)上递增,
结合图象可得: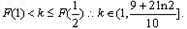
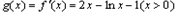 ,则
,则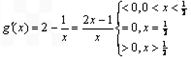 ,
,所以g(x)在
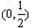 单调递减,在
单调递减,在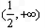 单调递增,
单调递增,则g(x)的最小值为
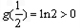 .
. 所以
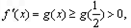 所以f(x)的单调递增区间是(0,+∞)
所以f(x)的单调递增区间是(0,+∞) 【另解】 ∵
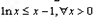 ,∴
,∴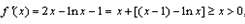
所以f(x)的单调递增区间是(0,+∞)
(Ⅱ)由(Ⅰ)得f(x)在区间
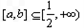 递增,
递增,∵f(x)在[a,b]上的值域是
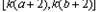
所以
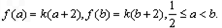
则
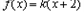 在
在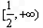 上至少有两个不同的正根,
上至少有两个不同的正根,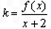 ,
,令
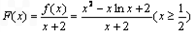 求导,得
求导,得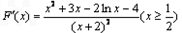 ,
,令
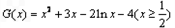 则
则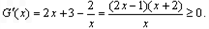
所以G(x)在
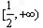 递增,
递增,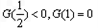 .
.当
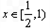 时,
时,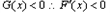 ,
,当
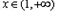 时,
时,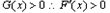
所以F(x)在
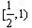 上递减,在(1,+∞)上递增,
上递减,在(1,+∞)上递增,结合图象可得:
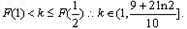

练习册系列答案
相关题目
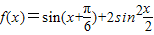 .
.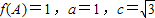 ,求b值.
,求b值.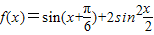 .
. ,求b值.
,求b值. .
. ,求
,求 的值.
的值. .
.
 时,求sin2x.
时,求sin2x. .
.