题目内容
已知函数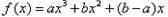 (
(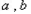 不同时为零的常数),导函数为
不同时为零的常数),导函数为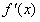
(Ⅰ)当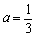 时,若存在
时,若存在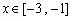 ,使得
,使得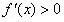 成立,求
成立,求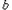 的取值范围;
的取值范围;
(Ⅱ)求证:函数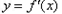 在
在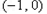 内至少有一个零点;
内至少有一个零点;
(Ⅲ)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线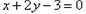 ,关于
,关于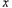 的方程
的方程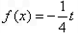 在
在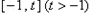 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围.
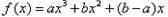 (
(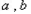 不同时为零的常数),导函数为
不同时为零的常数),导函数为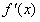
(Ⅰ)当
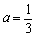 时,若存在
时,若存在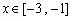 ,使得
,使得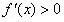 成立,求
成立,求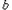 的取值范围;
的取值范围;(Ⅱ)求证:函数
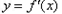 在
在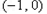 内至少有一个零点;
内至少有一个零点;(Ⅲ)若函数
 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线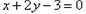 ,关于
,关于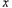 的方程
的方程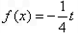 在
在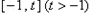 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围.解:(1 )当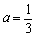 时,
时,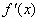 =
=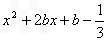 =
=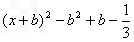 ,
,
其对称轴为直线 ,
,
当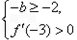 ,解得
,解得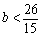 ,
,
当 ,
,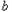 无解,
无解,
所以 的的取值范围为
的的取值范围为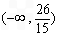
(2)因为 ,
,
当 时,
时, ,适合题意
,适合题意
当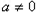 时,
时,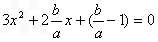 ,
,
令 ,则
,则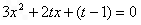 ,
,
令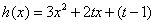 ,因为
,因为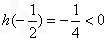 ,
,
当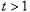 时,
时, ,
,
所以 在
在 内有零点.
内有零点.
当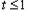 时,
时,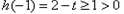 ,
,
所以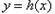 在(
在(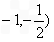 内有零点.
内有零点.
因此,当 时,
时,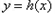 在
在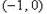 内至少有一个零点.
内至少有一个零点.
综上可知,函数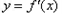 在
在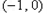 内至少有一个零点
内至少有一个零点
(3)因为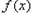 =
=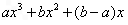 为奇函数,
为奇函数,
所以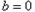 ,
,
所以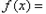
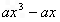 ,
,
又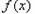 在
在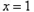 处的切线垂直于直线
处的切线垂直于直线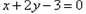 ,
,
所以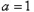 ,即
,即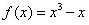
因为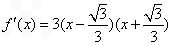
所以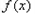 在
在 上是増函数,在
上是増函数,在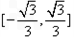 上是减函数,
上是减函数,
由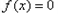 解得
解得 ,
,
如图所示,
当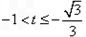 时,
时,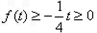 ,即
,即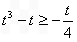 ,解得
,解得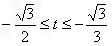 ;
;
当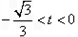 时,
时,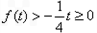 ,解得
,解得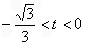 ;
;
当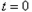 时,显然不成立;
时,显然不成立;
当 时,
时, ,即
,即 ,解得
,解得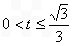 ;
;
当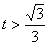 时,
时,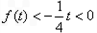 ,故
,故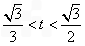 .
.
所以所求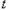 的取值范围是
的取值范围是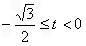 或
或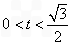
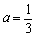 时,
时,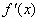 =
=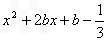 =
=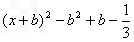 ,
,其对称轴为直线
 ,
,当
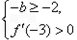 ,解得
,解得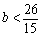 ,
,当
 ,
,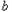 无解,
无解,所以
 的的取值范围为
的的取值范围为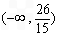
(2)因为
 ,
,当
 时,
时, ,适合题意
,适合题意当
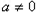 时,
时,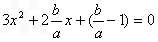 ,
,令
 ,则
,则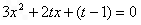 ,
,令
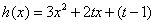 ,因为
,因为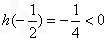 ,
,当
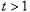 时,
时, ,
,所以
 在
在 内有零点.
内有零点.当
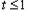 时,
时,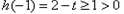 ,
,所以
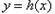 在(
在(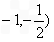 内有零点.
内有零点. 因此,当
 时,
时,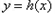 在
在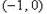 内至少有一个零点.
内至少有一个零点.综上可知,函数
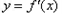 在
在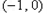 内至少有一个零点
内至少有一个零点(3)因为
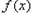 =
=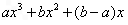 为奇函数,
为奇函数,所以
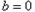 ,
, 所以
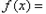
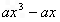 ,
,又
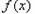 在
在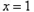 处的切线垂直于直线
处的切线垂直于直线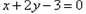 ,
,所以
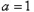 ,即
,即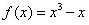
因为
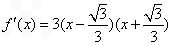
所以
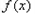 在
在 上是増函数,在
上是増函数,在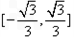 上是减函数,
上是减函数,由
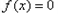 解得
解得 ,
,如图所示,
当
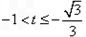 时,
时,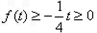 ,即
,即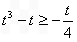 ,解得
,解得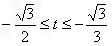 ;
;当
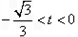 时,
时,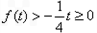 ,解得
,解得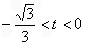 ;
;当
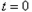 时,显然不成立;
时,显然不成立;当
 时,
时, ,即
,即 ,解得
,解得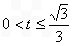 ;
;当
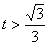 时,
时,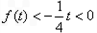 ,故
,故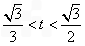 .
.所以所求
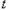 的取值范围是
的取值范围是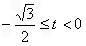 或
或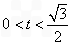


练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
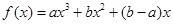 (
(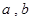 不同时为零的常数),导函数为
不同时为零的常数),导函数为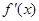 .
.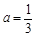 时,若存在
时,若存在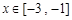 使得
使得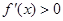 成立,求
成立,求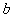 的取值范围;
的取值范围;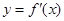 在
在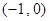 内至少有一个零点;
内至少有一个零点;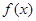 为奇函数,且在
为奇函数,且在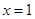 处的切线垂直于直线
处的切线垂直于直线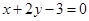 ,关于
,关于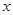 的方程
的方程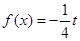 在
在 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数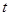 的取值范围.
的取值范围.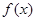 ,(
,(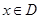 ),若同时满足以下条件:
),若同时满足以下条件: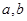 ]
]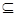 D,使
D,使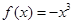 符合条件②的区间[
符合条件②的区间[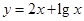 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[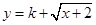 是闭函数,求实数
是闭函数,求实数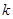 的取值范围.
的取值范围.