��Ŀ����
��֪����f��x����ͼ����[a��b]���������ϣ����壺  ��
�� ������min{f��x��|x��D}��ʾ����f��x����D�ϵ���Сֵ��max{f��x��|x��D}��ʾ����f��x����D�ϵ����ֵ����������С������k��ʹ��f2��x��-f1��x����k��x-a�����������x��[a��b]��������ƺ���f��x��Ϊ[a��b]�ϵġ�k��������������
������min{f��x��|x��D}��ʾ����f��x����D�ϵ���Сֵ��max{f��x��|x��D}��ʾ����f��x����D�ϵ����ֵ����������С������k��ʹ��f2��x��-f1��x����k��x-a�����������x��[a��b]��������ƺ���f��x��Ϊ[a��b]�ϵġ�k��������������
��1����f��x��=cosx��x��[0����]����д��f1��x����f2��x���ı���ʽ��
��2����֪����f��x��=x2��x��[-1��4]�����ж�f��x���Ƿ�Ϊ[-1��4]�ϵġ�k������������������ǣ������Ӧ��k��������ǣ���˵�����ɣ�
��3����֪ ������f��x��=-x3+3x2��[0��b]�ϵ�2��������������b��ȡֵ��Χ
������f��x��=-x3+3x2��[0��b]�ϵ�2��������������b��ȡֵ��Χ
 ��
�� ������min{f��x��|x��D}��ʾ����f��x����D�ϵ���Сֵ��max{f��x��|x��D}��ʾ����f��x����D�ϵ����ֵ����������С������k��ʹ��f2��x��-f1��x����k��x-a�����������x��[a��b]��������ƺ���f��x��Ϊ[a��b]�ϵġ�k��������������
������min{f��x��|x��D}��ʾ����f��x����D�ϵ���Сֵ��max{f��x��|x��D}��ʾ����f��x����D�ϵ����ֵ����������С������k��ʹ��f2��x��-f1��x����k��x-a�����������x��[a��b]��������ƺ���f��x��Ϊ[a��b]�ϵġ�k����������������1����f��x��=cosx��x��[0����]����д��f1��x����f2��x���ı���ʽ��
��2����֪����f��x��=x2��x��[-1��4]�����ж�f��x���Ƿ�Ϊ[-1��4]�ϵġ�k������������������ǣ������Ӧ��k��������ǣ���˵�����ɣ�
��3����֪
 ������f��x��=-x3+3x2��[0��b]�ϵ�2��������������b��ȡֵ��Χ
������f��x��=-x3+3x2��[0��b]�ϵ�2��������������b��ȡֵ��Χ�⣺��1 ��������ɵã� ��
�� ��
��
��2�� ��
�� ��
��
�� ʱ��
ʱ�� �� k��1-x,k��2
�� k��1-x,k��2
�� ʱ��1��k(x+1),��k��
ʱ��1��k(x+1),��k�� ,��k��1
,��k��1
�� ʱ��x2��k(x+1)��k��
ʱ��x2��k(x+1)��k�� ��
�� ��
��
������ ��ʹ��
��ʹ�� ��[-1,4]�ϵġ�4��������������
��[-1,4]�ϵġ�4��������������
��3�� ����
���� ��
�� ��
�� ��
�� �ı仯������£�
�ı仯������£�
��f��x��=0��x=0��x=3��
��i����b��2ʱ��f��x��=��[0,b]�ϵ���������
��ˣ� ��
�� ��
��
��Ϊ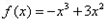 ��[0,b]�ϵġ���
��[0,b]�ϵġ���
���ԣ��� ��x��[0,b]�������
��x��[0,b]�������
�ڴ���x��[0,b]��ʹ�� ������
������
�ټ��� ��x��[0,b]�������
��x��[0,b]�������
�� ���0��x��1��x��2��
���0��x��1��x��2��
Ҫʹ ��x��[0,b]�����������ֻ��
��x��[0,b]�����������ֻ�� ��
��
�ڼ�������x��[0,b]��ʹ�� ������
������
�� ���
��� ��
�� ��
��
���ԣ�ֻ�� ��
��
�ۺϢ٢ڿɵ� ��
��
��i i ���� ʱ��f��x����[0,2]�ϵ�����������[2,b]�ϵ����ݼ���
ʱ��f��x����[0,2]�ϵ�����������[2,b]�ϵ����ݼ���
��ˣ� ��
�� ��
�� ��
��
��Ȼ��x=0ʱ�� ��������
��������
��i i i���� ʱ��f��x����[0,2]�ϵ�����������[2,b]�ϵ����ݼ���
ʱ��f��x����[0,2]�ϵ�����������[2,b]�ϵ����ݼ���
��ˣ� ��
�� ��
�� ��
��
��Ȼ��x=0ʱ�� ��������
��������
�ۺϣ�i����i i����i i i���ɵã� ��
��

��ϰ��ϵ�д�
�����Ŀ
��֪����f��x����ͼ�����ֱ��x=2�Գƣ��ҵ�x��2ʱ�䵼����f�䣨x������xf�䣨x����2f�䣨x������2��a��4�������б�ʾ��С��ϵ��ʽ����ȷ���ǣ�������
| A��f��2a����f��3����f��log2a�� | B��f(3)��f(log2a)��f(2a) | C��f(log2a)��f(3)��f(2a) | D��f(log2a)��f(2a)��f(3) |
 ��2011•����һģ����֪����f��x����ͼ����㣨
��2011•����һģ����֪����f��x����ͼ����㣨