用数学归纳法证明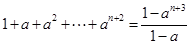 (
(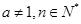 ),在验证当n=1时,等式左边应为
),在验证当n=1时,等式左边应为
| A.1 | B.1+a | C.1+a+a2 | D.1+a+a2+a3 |
用反证法证明“若a,b,c<3,则a,b,c中至少有一个小于1”时,“假设”应为
| A.假设a,b,c至少有一个大于1 | B.假设a,b,c都大于1 |
| C.假设a,b,c至少有两个大于1 | D.假设a,b,c都不小于1 |
在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ”的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ”中应用了( )
| A.分析法 |
| B.综合法 |
| C.分析法和综合法综合使用 |
| D.间接证法 |
三段论:“①所有的中国人都坚强不屈;②玉树人是中国人;③玉树人一定坚强不屈”中,其中“大前提”和“小前提”分别是( )
| A.①② | B.①③ |
| C.②③ | D.②① |
推理“①矩形是平行四边形;②正方形是矩形;③正方形是平行四边形”中的小前提是( )
| A.① | B.② |
| C.③ | D.以上均错 |
已知f(x+1)= ,f(1)=1(x∈N*),猜想f(x)的表达式为( )
,f(1)=1(x∈N*),猜想f(x)的表达式为( )
A.f(x)= | B.f(x)= |
C.f(x)= | D.f(x)= |
下列推理中属于归纳推理且结论正确的是( )
| A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2 |
| B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆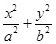 =1(a>b>0)的面积S=πab =1(a>b>0)的面积S=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n |
观察下列事实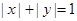 的不同整数解
的不同整数解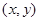 的个数为4,
的个数为4,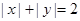 的不同整数解
的不同整数解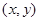 的个数为8,
的个数为8,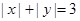 的不同整数解
的不同整数解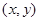 的个数为12,……,则
的个数为12,……,则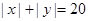 的不同整数解
的不同整数解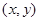 的个数为( )
的个数为( )
| A.76 | B.80 | C.86 | D.92 |
下面是一段演绎推理:
如果直线平行于平面,则这条直线平行于平面内的所有直线;
已知直线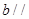 平面
平面 ,直线
,直线 平面
平面 ;
;
所以直线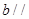 直线
直线 ,在这个推理中( )
,在这个推理中( )
| A.大前提正确,结论错误 |
| B.小前提与结论都是错误的 |
| C.大、小前提正确,只有结论错误 |
| D.大前提错误,结论错误 |
