题目内容
用反证法证明“若a,b,c<3,则a,b,c中至少有一个小于1”时,“假设”应为
| A.假设a,b,c至少有一个大于1 | B.假设a,b,c都大于1 |
| C.假设a,b,c至少有两个大于1 | D.假设a,b,c都不小于1 |
D
解析试题分析:“a,b,c中至少有一个小于1”的反面是“假设a,b,c都不小于1”,故选D。
考点:反证法
点评:本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A.假设三内角都不大于60度; | B.假设三内角都大于60度; |
| C.假设三内角至多有一个大于60度; | D.假设三内角至多有两个大于60度。 |
在应用数学归纳法证明凸n变形的对角线为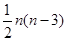 条时,第一步检验n等于( )
条时,第一步检验n等于( )
| A.1 | B.2 | C.3 | D.0 |
下列推理合理的是( )
A.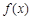 是增函数,则 是增函数,则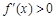 |
B.因为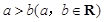 ,则 ,则 |
C.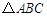 为锐角三角形,则 为锐角三角形,则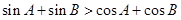 |
D.直线 ,则 ,则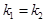 |
如下图,根据图中的数构成的规律,a所表示的数是( ) 
| A.12 | B.48 | C.60 | D.144 |
观察下列各式:72=49,73=343,74=2401,…,则72011的末两位数字为( )
| A.01 | B.43 |
| C.07 | D.49 |
已知f(x+1)= ,f(1)=1(x∈N*),猜想f(x)的表达式为( )
,f(1)=1(x∈N*),猜想f(x)的表达式为( )
A.f(x)= | B.f(x)= |
C.f(x)= | D.f(x)= |
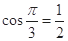

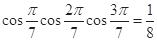
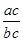 =
=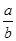 ”类比得到“
”类比得到“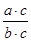 =
=