下列四种说法:
①命题“ x∈R,使得x2+1>3x”的否定是“
x∈R,使得x2+1>3x”的否定是“ x∈R,都有x2+1≤3x”;
x∈R,都有x2+1≤3x”;
②设 、q是简单命题,若“
、q是简单命题,若“ ”为假命题,则“
”为假命题,则“ ” 为真命题;
” 为真命题;
③把函数
 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数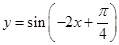
 的图像.其中所有正确说法的序号是( )
的图像.其中所有正确说法的序号是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
已知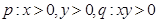 ,则p是q的( )
,则p是q的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是
A.命题“若 ,则 ,则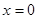 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.“若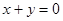 ,则 ,则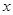 , ,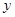 互为相反数”的逆命题为真命题 互为相反数”的逆命题为真命题 |
C.命题“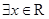 ,使得 ,使得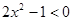 ”的否定是:“ ”的否定是:“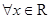 ,均有 ,均有 ” ” |
D.命题“若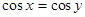 ,则 ,则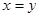 ”的逆否命题为真命题 ”的逆否命题为真命题 |
条件


 ,条件
,条件 sin
sin
 sin
sin ,那么条件
,那么条件 是条件
是条件 的( ).
的( ).
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.非充分也非必要条件 |
命题“对任意的 ”的否定是( ).
”的否定是( ).
A.不存在 | B.存在 |
C.存在 | D.对任意的 |
关于 的一元二次方程
的一元二次方程 的两个根均在区间
的两个根均在区间 内的必要不充分条件是
内的必要不充分条件是
A. | B. | C. | D. |
下列命题是真命题的是
①“若 ,则
,则 不全为零”的否命题;
不全为零”的否命题;
②“正六边形都相似”的逆命题;
③“若 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
④“若 是有理数,则
是有理数,则 是无理数”.
是无理数”.
| A.①④ | B.③④ | C.①③④ | D.①②③④ |
设 是平面
是平面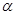 内两条不同的直线,
内两条不同的直线, 是平面
是平面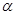 外的一条直线,则“
外的一条直线,则“ ,
, ”是“
”是“ ”的( )
”的( )
| A.充要条件 | B.充分而不必要的条件 |
| C.必要而不充分的条件 | D.既不充分也不必要的条件 |
已知p:x2-x< 0,那么命题p的一个必要不充分条件是
| A.0 < x < 1 | B.-1< x < 1 |
C. < x < < x <  | D. < x < 2 < x < 2 |
 关于
关于 的方程
的方程 有实根,命题
有实根,命题 关于
关于 在
在 上为增函数,若“
上为增函数,若“ 或
或 ”为真命题,“
”为真命题,“ 取值范围为( )
取值范围为( )


