题目内容
关于
的一元二次方程
的两个根均在区间
内的必要不充分条件是
A． | B． | C． | D． |
D
解析试题分析：因为关于的一元二次方程的两个根均在区间，则结合图像可知， f(x)=
需要满足f(-2）>0,f(4)>0, 
,且有对称轴x=a满足在-2<a<4，解得可知为-1<a<3,即为充要条件，那么其必要不充分条件的集合要包含-1<a<3，因此满足题意的只有选项D.
考点：本试题主要考查了一元二次方程的根与系数的关系的运用。
点评：解决该试题先分析使得方程两个根都在区间（-2,4）内时的充要条件，参数a满足的不等式。
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
已知P：
，Q：
, 则下列判断正确的是（ ）
A．“P或Q”为真，“ p”为真 | B．“P或Q”为假，“p”为真 |
| C．“P且Q”为真，“p”为假 | D．“P且Q”为假，“p”为假 |
若命题“
”为假，且“
”为假，则( )
A． 或 为假 | B．假 |
| C．真 | D．不能判断的真假 |
命题“
，
≥
”的否定是（ ）
A． ，≤ | B．，≥ |
C．， | D．， |
“
”是“方程
表示双曲线”的（ ）.
| A．充分不必要条件 | B．必要不充分条件 |
| C．既不充分也不必要条件 | D．充要条件 |
下列四种说法：
①命题“
x∈R，使得x2＋1＞3x”的否定是“
x∈R，都有x2＋1≤3x”；
②设
、q是简单命题，若“
”为假命题，则“
” 为真命题；
③把函数
的图像上所有的点向右平移
个单位即可得到函数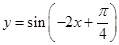
的图像．其中所有正确说法的序号是（ ）
| A．①② | B．②③ | C．①③ | D．①②③ |
设
，
，则 “
”是“
”的（ ）
| A．充分但不必要条件 | B．必要但不充分条件 |
| C．充要条件 | D．既不充分也不必要的条件 |
命题“
”的否定是
| A． | B． |
C． | D． |
下列命题错误的是 （ ）
A．命题“若 有实数根”的逆否命题为真命题 |
B．“ ”是“ ”的充分不必要条件 |
C．若 为假命题，则p、q均可能为假命题 |
D．命题 “ ，使得 ”的否定 为假命题 |