题目内容
下列四种说法:
①命题“ x∈R,使得x2+1>3x”的否定是“
x∈R,使得x2+1>3x”的否定是“ x∈R,都有x2+1≤3x”;
x∈R,都有x2+1≤3x”;
②设 、q是简单命题,若“
、q是简单命题,若“ ”为假命题,则“
”为假命题,则“ ” 为真命题;
” 为真命题;
③把函数
 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数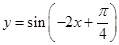
 的图像.其中所有正确说法的序号是( )
的图像.其中所有正确说法的序号是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
D
解析试题分析:①∵命题“?x∈R,使得x2+1>3x”,知“存在”的否定词为“任意”,
∴命题的否定为“?x∈R,都有x2+1≤3x”;故①正确;
②∵“p∪q”为假命题,∴p和q都为假命题,∴“¬p与¬q都为真命题,∴¬p∩¬q为真,故②正确;
③∵把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移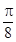 个单位,∴y=sin[-2(x-
个单位,∴y=sin[-2(x-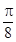 )]=sin(
)]=sin( -x),故③正确;
-x),故③正确;
故答案为①②③;选D.
考点:本试题主要考查了命题的否定、复合命题的真假判断以及三角函数的图象,是一道基础题。
点评:①根据命题否定的规则进行判断;②已知p、q是简单命题,若“p∨q”为假命题,可得p与q都为假命题,然后再进行判断;③把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移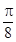 个单位,即把x变为x-
个单位,即把x变为x-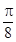 ,代入化简进行判断。
,代入化简进行判断。

练习册系列答案
相关题目
下列有关命题的说法正确的是
A.命题“若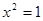 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若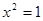 ,则 ,则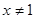 ”; ”; |
B.命题“  ”的否定是“ ”的否定是“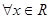 , ,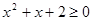 ,”; ,”; |
C.命题“若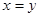 ,则 ,则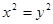 ”的逆否命题是假命题 ; ”的逆否命题是假命题 ; |
D.已知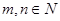 ,命题“若 ,命题“若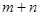 是奇数,则 是奇数,则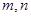 这两个数中一个为奇数,另一个为偶数”的逆命题为假命题. 这两个数中一个为奇数,另一个为偶数”的逆命题为假命题. |
若命题“ ”为假,且
”为假,且 为假,则( )
为假,则( )
A.“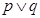 ”为假 ”为假 | B. 假 假 | C. 真 真 | D. 假 假 |
若 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
关于 的一元二次方程
的一元二次方程 的两个根均在区间
的两个根均在区间 内的必要不充分条件是
内的必要不充分条件是
A. | B. | C. | D. |
下列说法中,正确的是
A.命题“若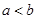 ,则 ,则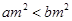 ”的否命题是假命题. ”的否命题是假命题. |
B.设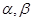 为两个不同的平面,直线 为两个不同的平面,直线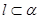 ,则 ,则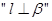 是 是 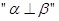 成立的充分不必要条件. 成立的充分不必要条件. |
C.命题“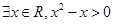 ”的否定是“ ”的否定是“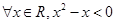 ”. ”. |
D.已知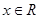 ,则“ ,则“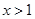 ”是“ ”是“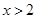 ”的充分不必要条件. ”的充分不必要条件. |
下列说法中,正确的是
A.命题“若 ,则 ,则 ”的逆命题是真命题 ”的逆命题是真命题 |
B.命题“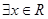 ,使得 ,使得 ”的否定是:“ ”的否定是:“  ,都有 ,都有 或 或 ” ” |
C.命题“ 或 或 ”为真命题,则命题“ ”为真命题,则命题“ ”和命题“ ”和命题“ ”均为真命题 ”均为真命题 |
D.已知 ,则“ ,则“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
下列说法错误的是
A.若命题 ,则 ,则  |
B.命题“若 ,则 ,则 ”的否命题是:“若 ”的否命题是:“若 ,则 ,则 ” ” |
C.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
D.若命题“ ”与命题“ ”与命题“ 或 或 ”都是真命题,那么命题 ”都是真命题,那么命题 一定是真命题 一定是真命题 |
给出以下四个命题:
①若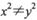 ,则
,则 或
或
②若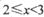 ,则
,则
③若a,b全为零,则
④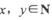 ,若
,若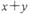 是奇数,则x,y中一个是奇数,一个是偶数.
是奇数,则x,y中一个是奇数,一个是偶数.
那么下列说法错误的是 ( )
| A.①为假命题 | B.②的逆命题为假 |
| C.③的否命题为真 | D.④的逆否命题为真 |