题目内容
5.已知△ABC中,AC=$\sqrt{2}$,BC=$\sqrt{6}$,∠ACB=$\frac{π}{6}$,若线段BA的延长线上存在点D,使∠BDC=$\frac{π}{4}$,则CD=$\sqrt{3}$.分析 在△ABC中,由余弦定理可得AB,进而可求∠B,在△ACD中,由正弦定理可得CD的值.
解答 解:∵AC=$\sqrt{2}$,BC=$\sqrt{6}$,∠ACB=$\frac{π}{6}$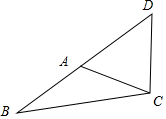
在△ABC中,由余弦定理可得:
AB2═BC2+AC2-2BC•AC•cos∠ACB=2+6-2×$\sqrt{2}$×$\sqrt{6}$×$\frac{\sqrt{3}}{2}$=2,
∴AB=$\sqrt{2}$
∴∠B=∠ACB=$\frac{π}{6}$,
∴∠DAC=∠B+∠ACB=$\frac{π}{3}$,
在△ACD中,由正弦定理可得$\frac{AC}{sin∠ADC}$=$\frac{CD}{sin∠DAC}$,
∴CD=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}$=$\sqrt{3}$
故答案为:$\sqrt{3}$
点评 本题主要考查了余弦定理,正弦定理在解三角形中的应用,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
相关题目