题目内容
14.已知函数$f(x)=ln({x+\frac{1}{a}})-ax$(a∈R,且a≠0).(1)讨论f(x)的单调区间;
(2)若直线y=ax的图象恒在函数y=f(x)图象的上方,求a的取值范围.
分析 (1)求出函数的定义域,求出导函数,根据导函数讨论参数a,得出函数的单调区间;
(2)构造函数令h(x)=ax-f(x),则$h(x)=2ax-ln({x+\frac{1}{a}})$.问题转化为h(x)>0恒成立时a的取值范围.对参数a进行分类讨论,利用导函数得出函数的最值即可.
解答 解:(1)f(x)的定义域为$({-\frac{1}{a},+∞})$,且$f'(x)=\frac{1}{{x+\frac{1}{a}}}-a=-\frac{{{a^2}x}}{ax+1}$.
①当a<0时,∵$x>-\frac{1}{a}$,∴ax<-1,∴f'(x)>0,函数在$({-\frac{1}{a},+∞})$是增函数;
②当a>0时,ax+1>0,在区间$({-\frac{1}{a},0})$上,f'(x)>0;在区间(0,+∞)上,f'(x)<0.
所以f(x)在区间$({-\frac{1}{a},0})$上是增函数;在区间(0,+∞)上是减函数.
(2)令h(x)=ax-f(x),则$h(x)=2ax-ln({x+\frac{1}{a}})$.
问题转化为h(x)>0恒成立时a的取值范围.
当a<0时,取$x=e-\frac{1}{a}$,则h(x)=2ae-3<0,不合题意.
当a>0时,h(x)=ax-f(x),则$h(x)=2ax-ln({x+\frac{1}{a}})$.
由于$h'(x)=2a-\frac{1}{{x+\frac{1}{a}}}=\frac{{2a({x+\frac{1}{2a}})}}{{x+\frac{1}{a}}}$,
所以在区间$({-\frac{1}{a},-\frac{1}{2a}})$上,h'(x)<0;在区间$({-\frac{1}{2a},+∞})$上,h'(x)>0.
所以h(x)的最小值为$h({-\frac{1}{2a}})$,
所以只需$h({-\frac{1}{2a}})>0$,即$2a•({-\frac{1}{2a}})-ln({-\frac{1}{2a}+\frac{1}{a}})>0$,
所以$ln\frac{1}{2a}<-1$,
所以$a>\frac{e}{2}$.
点评 本题考查了导函数的综合应用,难点是对参数的分类讨论和构造函数,把恒成立问题转换为最值问题.

| A. | $\frac{π}{9}$ | B. | $\frac{5π}{18}$ | C. | $\frac{7π}{18}$ | D. | $\frac{11π}{18}$ |
| x | 4 | 6 | 8 | 10 | 12 |
| y | 1 | 2 | 3 | 5 | 6 |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
| 学校 | A | B | C | D |
| 语文(x分) | 118 | 120 | 114 | 112 |
| 数学 (y分) | 116 | 123 | 114 | 119 |
(Ⅱ)依据调查表,怀化市的这所学校从A、B、C、D四所大学任选两所,求选出的这两所学校的语文和数学控分都低于120分的概率.
(附:线性回归方程$\hat y=\hat bx+\hat a$中,$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}\\ \hat a=\overline y-\hat b×\overline x\end{array}\right.$)
| 学生 学科 | A | B | C | D | E |
| 数学成绩(x) | 88 | 76 | 73 | 66 | 63 |
| 物理成绩(y) | 78 | 65 | 71 | 64 | 61 |
(2)求物理成绩y对数学成绩x的线性回归方程:
(3)一名学生的数学成绩为96分,试预测他的物理成绩.
参考数据:$\sum_{i=1}^5{{x_i}{y_i}}=25054,\sum_{i=1}^5{{x_i}^2}=27174$.
| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
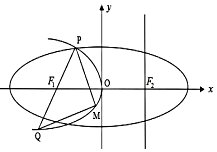 如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动. 如图所示,某幼儿园有一个游乐场ABCD,其中AB=50米,BC=40米,由于幼儿园招生规模增大,需将该游乐场扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ(弧度),EF的长为y米.
如图所示,某幼儿园有一个游乐场ABCD,其中AB=50米,BC=40米,由于幼儿园招生规模增大,需将该游乐场扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ(弧度),EF的长为y米.