题目内容
已知集合A={x|y=log2（x-1）}，B={x|x2-2x-3≤0}，则A∩B=（ ）
| A、[-1，3] |
| B、[1，3] |
| C、（-1，3] |
| D、（1，3] |
考点：交集及其运算
专题：集合
分析：求出A中x的范围确定出A，求出B中不等式的解集确定出B，求出两集合的交集即可．
解答：
解：由A中y=log2（x-1），得到x-1＞0，即x＞1，
∴A=（1，+∞），
由B中不等式变形得：（x-3）（x+1）≤0，
解得：-1≤x≤3，即B=[-1，3]，
则A∩B=（1，3]，
故选：D．
∴A=（1，+∞），
由B中不等式变形得：（x-3）（x+1）≤0，
解得：-1≤x≤3，即B=[-1，3]，
则A∩B=（1，3]，
故选：D．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
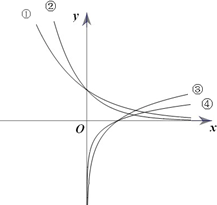如图，设实数a，b，c，d＞0，且不等于1，曲线①，②，③，④分别表示函数y=ax，y=bx，y=logcx，y=logdx在同一坐标系中的图象，则a，b，c，d的大小顺序为
