题目内容
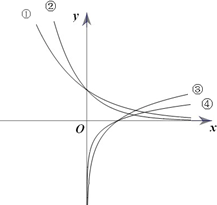 如图,设实数a,b,c,d>0,且不等于1,曲线①,②,③,④分别表示函数y=ax,y=bx,y=logcx,y=logdx在同一坐标系中的图象,则a,b,c,d的大小顺序为
如图,设实数a,b,c,d>0,且不等于1,曲线①,②,③,④分别表示函数y=ax,y=bx,y=logcx,y=logdx在同一坐标系中的图象,则a,b,c,d的大小顺序为考点:对数函数的图像与性质,指数函数的图像与性质
专题:函数的性质及应用
分析:根据指数函数的和对数的函数的图象和性质判断即可.
解答:
解:由函数的图象可得①y=ax 是减函数,②y=bx是减函数,故底数a,b都是大于0且小于1的实数.
作出直线x=1和函数①②图象的交点,可得a>b,故0<b<a<1.
由函数的图象可得函数③y=logcx 和④y=logdx是增函数,故底数c,d都是大于1的实数.
作出直线y=1和函数③④图象的交点,可得d>c,故有 d>c>1.
综上可得 d>c>a>b
故答案为:d>c>a>b
作出直线x=1和函数①②图象的交点,可得a>b,故0<b<a<1.
由函数的图象可得函数③y=logcx 和④y=logdx是增函数,故底数c,d都是大于1的实数.
作出直线y=1和函数③④图象的交点,可得d>c,故有 d>c>1.
综上可得 d>c>a>b
故答案为:d>c>a>b
点评:本题主要考查了指数函数和对数函数的图象和性质,属于基础题

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知0为坐标原点,向量
=(1,3),
=(3,-1)且
=2
,则点P的坐标为( )
| OA |
| OB |
| AP |
| PB |
| A、(2,-4) | ||||
B、(
| ||||
C、(
| ||||
| D、(-2,4) |
已知集合A={x|y=log2(x-1)},B={x|x2-2x-3≤0},则A∩B=( )
| A、[-1,3] |
| B、[1,3] |
| C、(-1,3] |
| D、(1,3] |