题目内容
已知sinα=
,sin(α-β)=
,且α,β∈(0,
).求:
(Ⅰ)cos(2α-β)的值.
(Ⅱ)β的值.
2
| ||
| 5 |
| ||
| 10 |
| π |
| 2 |
(Ⅰ)cos(2α-β)的值.
(Ⅱ)β的值.
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:(Ⅰ)由已知可得cosα和sin(α-β)的值,可得cos(2α-β)=cos[α+(α-β)]=cosαcos(α-β)-sinαsin(α-β),代入化简可得;(Ⅱ)由(Ⅰ)可得cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β),代入化简可得其值,结合β的范围可得.
解答:
解:(Ⅰ)∵α,β∈(0,
),∴α-β∈(-
,
),
∵sinα=
,∴cosα=
=
,
∴cos(α-β)=
=
,
∴cos(2α-β)=cos[α+(α-β)]
=cosαcos(α-β)-sinαsin(α-β)
=
•
-
•
=
(Ⅱ)由(Ⅰ)可得cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)
=
•
+
•
=
,
又∵β∈(0,
),∴β=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∵sinα=
2
| ||
| 5 |
| 1-sin2α |
| ||
| 5 |
∴cos(α-β)=
| 1-sin2(α-β) |
3
| ||
| 10 |
∴cos(2α-β)=cos[α+(α-β)]
=cosαcos(α-β)-sinαsin(α-β)
=
| ||
| 5 |
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 10 |
(Ⅱ)由(Ⅰ)可得cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)
=
| ||
| 5 |
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
又∵β∈(0,
| π |
| 2 |
| π |
| 4 |
点评:本题考查两角和与差的三角函数公式,整体法是解决问题的关键,属中档题.

练习册系列答案
相关题目
如图所示,程序框图(算法流程图)的输出值s=( )


| A、-1 | B、0 | C、1 | D、3 |
 在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.
在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.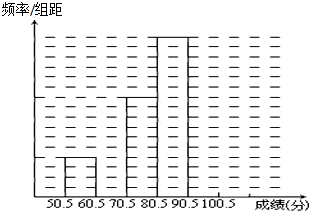 某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题: