题目内容
在锐角△ABC中,cos2C=-
.
(1)求sinC的值;
(2)当a=3,3sinC=
sinA时,求b的值.
| 1 |
| 9 |
(1)求sinC的值;
(2)当a=3,3sinC=
| 6 |
考点:正弦定理,二倍角的余弦
专题:解三角形
分析:(1)因为△ABC是锐角三角形,所以sinC>0,利用二倍角公式直接求出sinC即可;
(2)根据正弦定理求出c,利用余弦定理建立方程cosC=
=
,解出b=1或b=3,验证后舍去b=1即可.
(2)根据正弦定理求出c,利用余弦定理建立方程cosC=
| a2+b2-c2 |
| 2ab |
| 2 |
| 3 |
解答:
解:(1)∵△ABC是锐角三角形,
∴0<C<
,
∴sinC>0
∵cos2C=1-2sin2C=-
,
∴sinC=
.
(2)由正弦定理知3sinC=
sinA可化为,
3c=
a,
∵a=3,
∴c=
,
∵cosC=
=
,
∴cosC=
=
,
即b2-4b+3=0,
解得b=1或b=3,
∵b=1时,b2+c2=7<a2,与△ABC是锐角三角形矛盾,舍去.
∴b=3.
∴0<C<
| π |
| 2 |
∴sinC>0
∵cos2C=1-2sin2C=-
| 1 |
| 9 |
∴sinC=
| ||
| 3 |
(2)由正弦定理知3sinC=
| 6 |
3c=
| 6 |
∵a=3,
∴c=
| 6 |
∵cosC=
| 1-sin2C |
| 2 |
| 3 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| 2 |
| 3 |
即b2-4b+3=0,
解得b=1或b=3,
∵b=1时,b2+c2=7<a2,与△ABC是锐角三角形矛盾,舍去.
∴b=3.
点评:本题考查正弦定理和余弦定理的灵活应用,注意隐含三角形是锐角三角形的应用,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
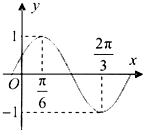 已知函数f(x)=sin(ωx+φ)(ω>0,φ<
已知函数f(x)=sin(ωx+φ)(ω>0,φ<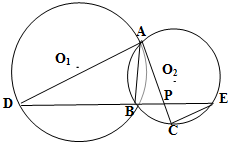 如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为