题目内容
3.若P(x,y)在不等式组$\left\{\begin{array}{l}{3x+y-8≤0}\\{x+2y-1≥0}\\{2x-y-2≥0}\end{array}\right.$所表示的平面区域内,则$\frac{1}{2}$x2+$\frac{1}{2}$y2的最大值为( )| A. | 4 | B. | 5 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{10}}{2}$ |
分析 作出可行域,目标函数z=$\frac{1}{2}$x2+$\frac{1}{2}$y2表示区域内的点到原点距离平方的一半,数形结合可得.
解答 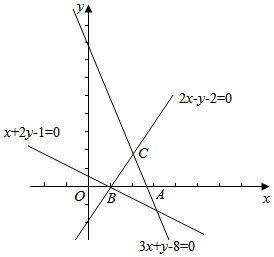 解:作出不等式组$\left\{\begin{array}{l}{3x+y-8≤0}\\{x+2y-1≥0}\\{2x-y-2≥0}\end{array}\right.$所对应的可行域(如图△ABC),
解:作出不等式组$\left\{\begin{array}{l}{3x+y-8≤0}\\{x+2y-1≥0}\\{2x-y-2≥0}\end{array}\right.$所对应的可行域(如图△ABC),
目标函数z=$\frac{1}{2}$x2+$\frac{1}{2}$y2表示区域内的点到原点距离平方的一半,
数形结合可知区域内的点A(3,1)满足目标函数取最大值,
联立$\left\{\begin{array}{l}{x+2y-1=0}\\{3x+y-8=0}\end{array}\right.$可解得A(3,1),
代值计算可得z的最大值为:$\frac{1}{2}$(32+12)=5,
故选:B.
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
13.若实数a,b∈R且a>b,则下列不等式恒成立的是( )
| A. | a2>b2 | B. | $\frac{a}{b}>1$ | C. | 2a>2b | D. | lg(a-b)>0 |
18.在△ABC中,若${a^2}-{b^2}=\sqrt{3}bc$且$\frac{c}{b}=2\sqrt{3}$,则角A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
15.已知命题p:若实数x,y满足x2+y2≠0,则x,y不全是0,命题q:若$\frac{1}{x}<1$则x>1,则下列命题中为真命题的是( )
| A. | (¬p)∨q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
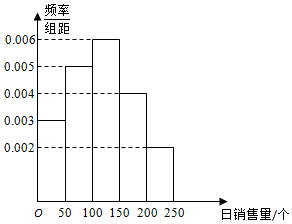 如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为9.
如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为9.