题目内容
13.若实数a,b∈R且a>b,则下列不等式恒成立的是( )| A. | a2>b2 | B. | $\frac{a}{b}>1$ | C. | 2a>2b | D. | lg(a-b)>0 |
分析 举特值可排除ABD,对于C可由指数函数的单调性得到.
解答 解:选项A,当a=-1且b=-2时,显然满足a>b但不满足a2>b2,故错误;
选项B,当a=-1且b=-2时,显然满足a>b但$\frac{a}{b}$=$\frac{1}{2}$,故错误;
选项C,由指数函数的单调性可知当a>b时,2a>2b,故正确;
选项D,当a=-1且b=-2时,显然满足a>b但lg(a-b)=lg1=0,故错误.
故选:C.
点评 本题考查不等式的运算性质,特值法是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.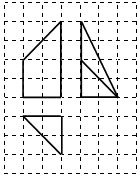 如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
 如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.已知各项均为正数的等比数列{an}中,a5•a6=4,则数列{log2an}的前10项和为( )
| A. | 5 | B. | 6 | C. | 10 | D. | 12 |
8.已知AB为圆O:(x-1)2+y2=1的直径,点P为直线x-y+1=0上任意一点,则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
18.某中学共8个艺术社团,现从中选10名同学组成新春社团慰问小组,其中书法社团需选出3名同学,其他各社团各选出1名同学,现从这10名同学中随机选取3名同学,到社区养老院参加“新春送欢乐”活动(每位同学被选到的可能性相同),则选出的3名同学来自不同社团的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{7}{24}$ | C. | $\frac{49}{60}$ | D. | $\frac{1}{10}$ |
2.若α是第二象限角,$tan(\frac{π}{3}+α)=\frac{4}{3}$,则$cos(\frac{π}{3}+α)$=( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $±\frac{3}{5}$ |
3.若P(x,y)在不等式组$\left\{\begin{array}{l}{3x+y-8≤0}\\{x+2y-1≥0}\\{2x-y-2≥0}\end{array}\right.$所表示的平面区域内,则$\frac{1}{2}$x2+$\frac{1}{2}$y2的最大值为( )
| A. | 4 | B. | 5 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{10}}{2}$ |