题目内容
将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为6的概率;
(2)两数之积是6的倍数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率.
(1)两数之和为6的概率;
(2)两数之积是6的倍数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:试验发生包含的所有事件总数为36,满足条件的事件可以通过列举得到事件数,根据古典概型公式得到结果.
解答:
解:将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件
(1)记“两数之和为6”为事件A,则事件A中含有(1,5),(2,4),(3,3),(5,1),(4,2)共5个基本事件,
∴P(A)=
,
(2)记“两数之积是6的倍数”为事件B,则事件B中含有(1,6),(2,6),(3,6),(4,6),(5,6),(6,6),(6,5),(6,4),(6,3),(6,2),(6,1),(2,3),(3,2),(3,4),(4,3)共15个基本事件,
∴P(A)=
=
,
(3)记“圆x2+y2=15的内部”为事件C.则x,y的值都小于
且x2+y2=15,则事件C中含有(1,1),(1,2),(2,2),(2,1),(1,3),(2,3),(3,2),(3,1)共8个基本事件,
∴P(C)=
=
.
(1)记“两数之和为6”为事件A,则事件A中含有(1,5),(2,4),(3,3),(5,1),(4,2)共5个基本事件,
∴P(A)=
| 5 |
| 36 |
(2)记“两数之积是6的倍数”为事件B,则事件B中含有(1,6),(2,6),(3,6),(4,6),(5,6),(6,6),(6,5),(6,4),(6,3),(6,2),(6,1),(2,3),(3,2),(3,4),(4,3)共15个基本事件,
∴P(A)=
| 15 |
| 36 |
| 5 |
| 12 |
(3)记“圆x2+y2=15的内部”为事件C.则x,y的值都小于
| 15 |
∴P(C)=
| 8 |
| 36 |
| 2 |
| 9 |
点评:本题是一个古典概型问题,古典概型要求能够列举出所有事件和发生事件的个数,本题可以列举出所有事件.是一个基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
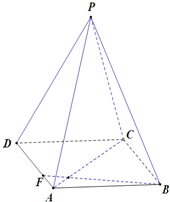 如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为
如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为 已知三棱柱ABC-A1B1C1中,D为线段A1C1中点.求证:BC1∥平面AB1D.
已知三棱柱ABC-A1B1C1中,D为线段A1C1中点.求证:BC1∥平面AB1D.