题目内容
15.设等比数列{an}的公比为q,前n项和为Sn,且a1>0,若S2>2a3,则q的取值范围是( )| A. | $(-1,0)∪(0,\frac{1}{2})$ | B. | $(-\frac{1}{2},0)∪(0,1)$ | C. | $(-1,\frac{1}{2})$ | D. | $(-\frac{1}{2},1)$ |
分析 根据题意,分析易得a1+a2>2a3,由等比数列通项公式可得a1+a1q>2a1q2,结合a1>0,可以变形1+q>2q2;解可得q的范围,即可得答案.
解答 解:根据题意,对于等比数列{an},有S2>2a3,
则有a1+a2>2a3,即a1+a1q>2a1q2;
又由a1>0,则有1+q>2q2;
解可得-$\frac{1}{2}$<q<1,
又由q≠0,
则q的取值范围是(-$\frac{1}{2}$,0)∪(0,1);
故选:B.
点评 本题考查等比数列的前n项和,注意运用本公式时注意公比q是否为1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知集合A={x|(x+1)(x-2)>0},B={x∈Z|x2-9≤0},则A∩B=( )
| A. | {0,1} | B. | (0,1) | C. | [-3,-1)∪(2,3] | D. | {-3,-2,3} |
7.圆x2+y2=1与直线xsinθ+y-1=0的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相切或相交 |
4.已知集合$A=\left\{{x\left|{\frac{x-1}{x+3}>0}\right.}\right\}$,$B=\left\{{y\left|{y=\sqrt{4-{x^2}}}\right.}\right\}$,则A∪B=( )
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3)∪(1,2] | C. | (-∞,-3)∪[0,+∞) | D. | (1,2] |
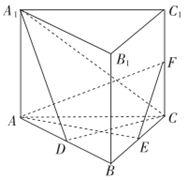 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.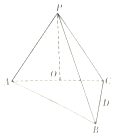 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.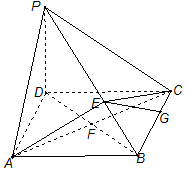 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点.