题目内容
5.已知首项为$\frac{3}{2}$的等比数列{an}的前n项和为Sn,n∈N*,且-2S2,S3,4S4成等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)对于数列$\left\{{A_n^{\;}}\right\}$,若存在一个区间M,均有Ai∈M,(i=1,2,3…),则称M为数列$\left\{{A_n^{\;}}\right\}$的“容值区间”,设${b_n}={S_n}+\frac{1}{S_n}$,试求数列{bn}的“容值区间”长度的最小值.
分析 (Ⅰ)设等比数列{an}的公比为q(q≠0),运用等差数列的中项的性质,以及等比数列的通项公式,解方程可得q,即可得到所求通项公式;
(Ⅱ)运用等比数列的求和公式,讨论n为偶数,n为奇数,结合数列的单调性,以及“容值区间”的定义,即可得到所求区间的最小值.
解答 解:(Ⅰ)设等比数列{an}的公比为q(q≠0),
由-2S2,S3,4S4成等差数列,
知-2S2+4S4=2S3,
则$-2({\frac{3}{2}+\frac{3}{2}q})+4({\frac{3}{2}+\frac{3}{2}q+\frac{3}{2}{q^2}+\frac{3}{2}{q^3}})=2({\frac{3}{2}+\frac{3}{2}q+\frac{3}{2}{q^2}})$,
化简得3q2+6q3=0,解得$q=-\frac{1}{2}$,
则${a_n}=\frac{3}{2}•{({-\frac{1}{2}})^{n-1}}$;
(Ⅱ)由(Ⅰ)可知${S_n}=1-{({-\frac{1}{2}})^n}$,
当n为偶数时,${S_n}=1-{({\frac{1}{2}})^n}$,易知Sn随n增大而增大,
∴${S_n}∈[{\frac{3}{4},1})$,此时${b_n}={S_n}+\frac{1}{S_n}∈({2,\frac{25}{12}}]$,
当n为奇数时,${S_n}=1+{({\frac{1}{2}})^n}$,易知Sn随n增大而减小,
∴${S_n}∈({1,\frac{3}{2}}]$,此时${b_n}={S_n}+\frac{1}{S_n}∈({2,\frac{13}{6}}]$,
又$\frac{13}{6}>\frac{25}{12}$,∴${b_n}∈({2,\frac{13}{6}}]$,
区间长度为$\frac{13}{6}$-2=$\frac{1}{6}$.
故数列{bn}的“容值区间”长度的最小值为$\frac{1}{6}$.
点评 本题考查等差数列的中项的性质和等比数列的通项公式,考查新定义的理解和运用,以及分类讨论的思想方法,注意运用单调性,考查化简整理的运算能力,属于中档题.

| A. | 1 | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
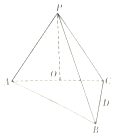 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.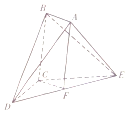 在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.
在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.