题目内容
20.已知点F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,点B是短轴顶点,直线BF2与椭圆C相交于另一点D.若△F1BD是等腰三角形,则椭圆C的离心率为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 由题意画出图形,结合已知求出|DF1|、|DF2|,再由余弦定理列式求得答案.
解答 解:如图,由椭圆定义可得:|DF1|+|DF2|=2a,∵△F1BD是等腰三角形,
∴|DF1|=|DB|=|DF2|+|BF2|,解得|DF2|=$\frac{1}{2}a$,|DF1|=$\frac{3}{2}a$.
又|BF1|=a,
∴cos∠F1DF2=$\frac{(\frac{3}{2}a)^{2}+(\frac{3}{2}a)^{2}-{a}^{2}}{2×\frac{3}{2}a×\frac{3}{2}a}=\frac{7}{9}$,
又cos∠F1DF2=$\frac{(\frac{3}{2}a)^{2}+(\frac{1}{2}a)^{2}-(2c)^{2}}{2×\frac{3}{2}a×\frac{1}{2}a}=\frac{7}{9}$,
∴$\frac{10}{4}{a}^{2}-4{c}^{2}=\frac{7}{6}{a}^{2}$,化简得:a2=3c2,得$e=\frac{\sqrt{3}}{3}$.
故选:B.
点评 本题考查椭圆的简单性质,考查了椭圆定义及余弦定理的应用,是中档题.

练习册系列答案
相关题目
11.数列{an}的前n项和Sn=n2-5n(n∈N*),若p-q=4,则ap-aq=( )
| A. | 20 | B. | 16 | C. | 12 | D. | 8 |
15.已知a,b,c分别为△ABC的三个内角A,B,C的对边,c=2,且sin2A+sin2B=sinAsinB+sin2C,则△ABC面积的最大值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
12.已知直线a,b以及平面α,β,则下列命题正确的是( )
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,b⊥α,则 a⊥b | ||
| C. | 若a∥b,b∥α,则a∥α | D. | 若a⊥α,b∥β,则 α⊥β |
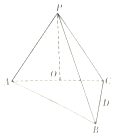 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.