题目内容
19.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别是F1、F2,离心率为$\frac{1}{2}$,以原点O为圆心,椭圆C的短半轴长为半径的圆与直线x+$\sqrt{2}$y-3=0相切.(1)求椭圆C的标准方程;
(2)动直线l;y=kx+m与椭圆C相切,分别过点F1、F2作直线垂直于l,垂足分别为D、E,求|F1D|+|F2E|的最小值.
分析 (1)由椭圆的离心率公式及点到直线的距离公式求得b的值,由a2=b2+c2,即可求得a和c的值,求得椭圆方程;
(2)过O做OP⊥l垂足为P,利用中位线定理2丨OP丨=|F1D|+|F2E|,则P位于短轴的顶点时,丨OP丨最小,即可求得|F1D|+|F2E|的最小值.
解答 解:(1)由椭圆的焦点在x轴上,椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,则a=2c,①
由圆x2+y2=b2与直线x+$\sqrt{2}$y-3=0相切,则圆心到直线x+$\sqrt{2}$y-3=0的距离等于半径d,
则b=$\frac{丨0-0-3丨}{\sqrt{{1}^{2}+(\sqrt{2})^{2}}}$=$\sqrt{3}$,
由a2=b2+c2,②
由①②可知:a=2,c=1,
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由题意得过:O做OP⊥l垂足为P,
∴2丨OP丨=|F1D|+|F2E|,
当丨OP丨=b时,丨OP丨最小
此时2丨OP丨=2$\sqrt{3}$
|F1D|+|F2E|的最小值为2$\sqrt{3}$,
综上所述,|F1D|+|F2E|的最小值为2$\sqrt{3}$.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查点到直线距离公式的应用,考查数形结合思想,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
9.设M={α|α=k•90°,k∈Z}∪{α|α=k•180°+45°,k∈Z},N={α|α=k•45°,k∈Z},则( )
| A. | M⊆N | B. | M?N | C. | M=N | D. | M∩N=Φ |
7.圆x2+y2=1与直线xsinθ+y-1=0的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相切或相交 |
4.已知集合$A=\left\{{x\left|{\frac{x-1}{x+3}>0}\right.}\right\}$,$B=\left\{{y\left|{y=\sqrt{4-{x^2}}}\right.}\right\}$,则A∪B=( )
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3)∪(1,2] | C. | (-∞,-3)∪[0,+∞) | D. | (1,2] |
11.数列{an}的前n项和Sn=n2-5n(n∈N*),若p-q=4,则ap-aq=( )
| A. | 20 | B. | 16 | C. | 12 | D. | 8 |
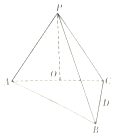 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.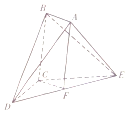 在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.
在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.