题目内容
4．已知三棱柱ABC-A′B′C′的底面为直角三角形，两条直角边AC和BC的长分别为4和3，侧棱AA′的长为10．（1）若侧棱AA′垂直于底面，求该三棱柱的表面积；
（2）若侧棱AA′与底面所成的角为60°，求该三棱柱的体积．
分析 （1）根据直三棱柱的表面积公式进行求解即可．
（2）作出棱柱的高，结合三棱柱的体积公式进行求解即可．
解答 
解：（1）因为侧棱AA′⊥底面ABC，所以三棱柱的高h等于侧棱AA′的长，
而底面三角形ABC的面积S=$\frac{1}{2}$AC•BC=6，
周长c=4+3+5=12，
于是三棱柱的表面积S全=ch+2S△ABC=132．
（2）如图，过A作平面ABC的垂线，垂足为H，A′H为三棱柱的高．
因为侧棱AA′与底面ABC所长的角为60°，
所以∠A′AH=60°，
又底面三角形ABC的面积S=6，故三棱柱的体积V=S•A′H=6×$5\sqrt{3}$=30$\sqrt{3}$．
点评 本题主要考查三棱柱的表面积和体积的计算，根据直三棱柱和斜三棱柱的特点和性质，结合棱柱的表面积和体积公式进行计算是解决本题的关键．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
9．凸四边形OABC中，$\overrightarrow{OB}=（2，4），\overrightarrow{AC}$=（-2，1），则该四边形的面积为（ ）
| A． | $\sqrt{5}$ | B． | $2\sqrt{5}$ | C． | 5 | D． | 10 |
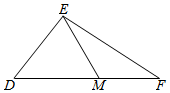如图所示，在△DEF中，M是在线段DF上，DE=3，DM=EM=2，sin∠F=$\frac{3}{5}$=，则边EF的长为$\frac{5\sqrt{7}}{4}$．
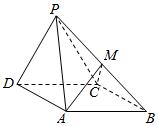如图，四棱锥P-ABCD中，底面ABCD是菱形，∠ADC=60°，面PCD⊥面ABCD，PC=PD=CD=2，点M为线段PB上异于P、B的点．