题目内容
8．已知向量|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°．（1）求$\overrightarrow{a}$•$\overrightarrow{b}$；
（2）若$\overrightarrow{c}$=2$\overrightarrow{a}$-$\overrightarrow{b}$，$\overrightarrow{d}$=$\overrightarrow{a}$+$λ\overrightarrow{b}$，且$\overrightarrow{c}$⊥$\overrightarrow{d}$，求实数λ的值．
分析 （1）根据平面向量的数量积定义计算；
（2）令$\overrightarrow{c}•\overrightarrow{d}=0$列方程解出λ．
解答 解：（1）$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos60°$=2×$3×\frac{1}{2}$=3．
（2）∵$\overrightarrow{c}$⊥$\overrightarrow{d}$，∴（2$\overrightarrow{a}-\overrightarrow{b}$）•（$\overrightarrow{a}+λ\overrightarrow{b}$）=0，
即2${\overrightarrow{a}}^{2}$+（2λ-1）$\overrightarrow{a}•\overrightarrow{b}$-$λ{\overrightarrow{b}}^{2}$=0，
∴8+3（2λ-1）-9λ=0，解得λ=$\frac{5}{3}$．
点评 本题考查了平面向量的数量积运算，属于基础题．
练习册系列答案
相关题目
20．三角形ABC中角A、B、C对边分别为a、b、c，且a=2，b=3，c=4．若长度为4的动线段PQ的中点恰为A点，则$\overrightarrow{BP}•\overrightarrow{CQ}$的最大值是（ ）
| A． | -$\frac{3}{2}$ | B． | $\frac{11}{2}$ | C． | $\frac{21}{2}$ | D． | $\frac{29}{2}$ |
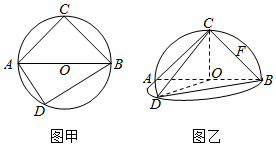如图甲：⊙O的直径AB=2，圆上两点C，D在直径AB的两侧，使∠CAB=$\frac{π}{4}$，∠DAB=$\frac{π}{3}$，沿直径AB折起，使两个半圆所在的平面互相垂直（如图乙），F为BC的中点，根据图乙解答下列各题：