题目内容
19.定义四个数a,b,c,d的二阶积和式$[\begin{array}{l}ab\\ cd\end{array}]=ad+bc$.九个数的三阶积和式可用如下方式化为二阶积和式进行计算:$[\begin{array}{l}{a_1}{a_2}{a_3}\\{b_1}{b_2}{b_3}\\{c_1}{c_2}{c_3}\end{array}]={a_1}×[\begin{array}{l}{b_2}{b_3}\\{c_2}{c_3}\end{array}]+{a_2}×[\begin{array}{l}{b_1}{b_3}\\{c_1}{c_3}\end{array}]+{a_3}×[\begin{array}{l}{b_1}{b_2}\\{c_1}{c_2}\end{array}]$.已知函数f(n)=$[\begin{array}{l}{n}&{2}&{-9}\\{n}&{1}&{n}\\{1}&{2}&{n}\end{array}]$
(n∈N*),则f(n)的最小值为-21.
分析 根据定义函数f(n)=$[\begin{array}{l}{n}&{2}&{-9}\\{n}&{1}&{n}\\{1}&{2}&{n}\end{array}]$=(-9)×$[\begin{array}{l}{n}&{1}\\{1}&{2}\end{array}]$+2×$[\begin{array}{l}{n}&{n}\\{1}&{n}\end{array}]$+n×$[\begin{array}{l}{1}&{n}\\{2}&{n}\end{array}]$=(-9)×(2n+1)+2(n2+n)+n(n+2n)=5n2-16n-9(n∈N*),根据二次函数求出最值.
解答 解:函数f(n)=$[\begin{array}{l}{n}&{2}&{-9}\\{n}&{1}&{n}\\{1}&{2}&{n}\end{array}]$=(-9)×$[\begin{array}{l}{n}&{1}\\{1}&{2}\end{array}]$+2×$[\begin{array}{l}{n}&{n}\\{1}&{n}\end{array}]$+n×$[\begin{array}{l}{1}&{n}\\{2}&{n}\end{array}]$=(-9)×(2n+1)+2(n2+n)+n(n+2n)=5n2-16n-9
∵n∈N*,∴n=2时,f(n)的最小值为-21
故答案为:-21
点评 本题考查了对新定义的理解,及二次函数最值问题,属于基础题,

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
14.复数$z=\frac{10i}{3+i}$(i为虚数单位)的虚部为( )
| A. | 1 | B. | 3 | C. | -3 | D. | $\frac{15}{4}$ |
8.等比数列{an}中,a1=3,a8=9,函数f(x)=x(x-a1)(x-a2)…(x-a8),则f'(0)=( )
| A. | 36 | B. | 39 | C. | 312 | D. | 315 |
9.已知集合M={x|x2<1},N={x|x≥0},则M∩N=( )
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|x≥0} | D. | {x|-1<x≤0} |
 在三棱柱ABC-A1B1C1中,侧面A1ABB1为矩形,AB=2,AA1=4,D在棱AA1上,且4AD=AA1,BD与AB1交于点O,且CO⊥平面A1ABB1.
在三棱柱ABC-A1B1C1中,侧面A1ABB1为矩形,AB=2,AA1=4,D在棱AA1上,且4AD=AA1,BD与AB1交于点O,且CO⊥平面A1ABB1.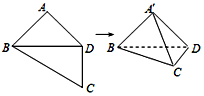 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).