题目内容
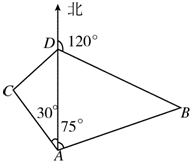
海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12
海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
| 6 |
| 3 |
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
考点:解三角形的实际应用
专题:应用题,解三角形
分析:(1)在三角形ABD中,利用正弦定理列出关系式,将各自的值代入求出AD的长,即可确定出货船的航行速度;
(2)在三角形ACD中,利用余弦定理列出关系式,将各自的值代入计算即可求出CD的长.
(2)在三角形ACD中,利用余弦定理列出关系式,将各自的值代入计算即可求出CD的长.
解答:
 解:(1)在△ABD中,∠ADB=60°,∴∠B=45°,
解:(1)在△ABD中,∠ADB=60°,∴∠B=45°,
由正弦定理,得
&;sinB=
,
即AD=
=
=24(海里),
(2)在△ACD中,∵AC=8
,∠CAD=30°,
∴由余弦定理得CD2=AD2+AC2-2AD•ACcos∠CAD=242+(8
)2-2×24×8
cos30°=192,
解得:CD=8
≈14(海里),
则灯塔C与D之间的距离约为14海里.
 解:(1)在△ABD中,∠ADB=60°,∴∠B=45°,
解:(1)在△ABD中,∠ADB=60°,∴∠B=45°,由正弦定理,得
| AD |
| AB |
| sin∠ADB |
即AD=
| ABsinB |
| sin∠ADB |
12
| ||||||
|
(2)在△ACD中,∵AC=8
| 3 |
∴由余弦定理得CD2=AD2+AC2-2AD•ACcos∠CAD=242+(8
| 3 |
| 3 |
解得:CD=8
| 3 |
则灯塔C与D之间的距离约为14海里.
点评:此题考查了正弦定理,余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键,属于基本知识的考查.

练习册系列答案
相关题目
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[0,1].
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性并试用定义证明;
(3)求g(x)的值域.
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性并试用定义证明;
(3)求g(x)的值域.
若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是( )
| A、(-∞,-2] |
| B、(-∞,-1] |
| C、[2,+∞) |
| D、[1,+∞) |
下列命题的说法错误的是( )
| A、命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
| B、若p∧q为假命题,则p,q均为假命题 |
| C、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| D、对于命题p:?x∈R,x2+x+1>0,则¬p:?x∈R,x2+x+1≤0 |
若一个几何体的主视图和左视图是边长为2的等边三角形,俯视图是一个圆,则这个几何体的体积是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、不能确定 |
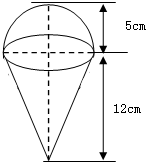 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14)