题目内容
已知函数f(x)=x3+bx2+cx+d在区间(-∞,0]和[6,8]上单调递增,在[0,2]上单调递减,其图象与x轴交于A,B,C三点,其中点B的坐标为(2,0).
(Ⅰ)求c的值;
(Ⅱ)求b的取值范围;
(Ⅲ)求|AC|的取值范围.
(Ⅰ)求c的值;
(Ⅱ)求b的取值范围;
(Ⅲ)求|AC|的取值范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)由已知得:f'(x)=3x2+2bx+c,由f'(0)=0得:c=0;
(Ⅱ)由(Ⅰ)得:f(x)=x3+bx2+d,由f(2)=0得f'(x)=3x2+2bx,解出即可;
(Ⅲ)设A(x1,0),C(x2,0),则f(x)=(x-2)(x-x1)(x-x2),表示出|AC|,求出即可.
(Ⅱ)由(Ⅰ)得:f(x)=x3+bx2+d,由f(2)=0得f'(x)=3x2+2bx,解出即可;
(Ⅲ)设A(x1,0),C(x2,0),则f(x)=(x-2)(x-x1)(x-x2),表示出|AC|,求出即可.
解答:
 解:(Ⅰ)由已知得:f'(x)=3x2+2bx+c,
解:(Ⅰ)由已知得:f'(x)=3x2+2bx+c,
由f'(0)=0得:c=0;
(Ⅱ)由(Ⅰ)得:f(x)=x3+bx2+d
由f(2)=0得:8+4b+d=0,
∴f(x)=x3+bx2-4b-8,f'(x)=3x2+2bx
令f'(x)=0得:x=0或x=-
b
由已知得:2≤-
b≤6,
∴-9≤b≤-3
所以,所求的b的取值范围是:[-9,-3];
(Ⅲ)设A(x1,0),C(x2,0),
则f(x)=(x-2)(x-x1)(x-x2)
=(x-2)[x2-x(x1+x2)+x1x2]
=x3-(x1+x2+2)x2+[x1x2+2(x1+x2)]x-2x1x2
又f(x)=x3+bx2-4b-8,
∴
,
∴
;
∴|AC|=|x1-x2|=
=
=
=
,
∵-9≤b≤-3,∴3≤|AC|≤
所以,|AC|的取值范围是[3,
].
 解:(Ⅰ)由已知得:f'(x)=3x2+2bx+c,
解:(Ⅰ)由已知得:f'(x)=3x2+2bx+c,由f'(0)=0得:c=0;
(Ⅱ)由(Ⅰ)得:f(x)=x3+bx2+d
由f(2)=0得:8+4b+d=0,
∴f(x)=x3+bx2-4b-8,f'(x)=3x2+2bx
令f'(x)=0得:x=0或x=-
| 2 |
| 3 |
由已知得:2≤-
| 2 |
| 3 |
∴-9≤b≤-3
所以,所求的b的取值范围是:[-9,-3];
(Ⅲ)设A(x1,0),C(x2,0),
则f(x)=(x-2)(x-x1)(x-x2)
=(x-2)[x2-x(x1+x2)+x1x2]
=x3-(x1+x2+2)x2+[x1x2+2(x1+x2)]x-2x1x2
又f(x)=x3+bx2-4b-8,
∴
|
∴
|
∴|AC|=|x1-x2|=
| (x1-x2)2 |
=
| (x1+x2)2-4x1x2 |
=
| b2-4b-12 |
=
| (b-2)2-16 |
∵-9≤b≤-3,∴3≤|AC|≤
| 105 |
所以,|AC|的取值范围是[3,
| 105 |
点评:本题主要考查三次函数的图象与性质和导数的应用,考查数形结合思想方法和运算求解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在平行四边形ABCD中,|AB|=3,|BC|=2,
如图,在平行四边形ABCD中,|AB|=3,|BC|=2,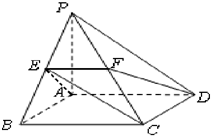 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.