题目内容
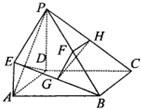 如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.(Ⅰ)求证:平面FGH∥平面PED
(Ⅱ)求平面FGH与平面PBC所成锐二面角的大小.
考点:用空间向量求平面间的夹角,平面与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)由三角形的中位线定理得到线线平行,然后直接利用线面平行的判定定理得到线面平行;
(Ⅱ)建立空间直角坐标系,根据两个平面的法向量所成的角与二面角相等或互补,由两个平面法向量所成的角求解二面角的大小.
(Ⅱ)建立空间直角坐标系,根据两个平面的法向量所成的角与二面角相等或互补,由两个平面法向量所成的角求解二面角的大小.
解答:
 (Ⅰ)证明:因为F,G分别为PB,BE的中点,所以FG∥PE.
(Ⅰ)证明:因为F,G分别为PB,BE的中点,所以FG∥PE.
又FG?平面PED,PE?平面PED,所以FG∥平面PED.
同理FH∥BC,
∵AD∥BC,
∴FH∥AD,
∵FH?平面PED,AD?平面PED,
∴FH∥平面PED,
∵FG∩FH=F,
∴平面FGH∥平面PED;
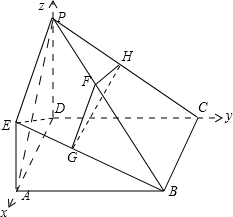
(Ⅱ)解:∵EA⊥平面ABCD,∴PD⊥平面ABCD,∴PD⊥AD,PD⊥CD.
又∵四边形ABCD是正方形,∴AD⊥CD.
如图建立空间直角坐标系,∵AD=PD=2EA,∴D(0,0,0),P(0,0,2),A(2,0,0),C(0,2,0),B(2,2,0),E(2,0,1).
∵F,G,H分别为PB,EB,PC的中点,∴F(1,1,1),G(2,1,0.5),H(0,1,1).
∴
=(-1,0,0.5),
=(-2,0,0.5),
设
=(x,y,z)为平面FGH的一个法向量,则
,
再令y1=1,得
=(0,1,0).
同理可得平面PBC的一个法向量为
=(0,1,1),
∴|cos<
,
>|=
.
∴平面FGH与平面PBC所成锐二面角的大小为
.
 (Ⅰ)证明:因为F,G分别为PB,BE的中点,所以FG∥PE.
(Ⅰ)证明:因为F,G分别为PB,BE的中点,所以FG∥PE.又FG?平面PED,PE?平面PED,所以FG∥平面PED.
同理FH∥BC,
∵AD∥BC,
∴FH∥AD,
∵FH?平面PED,AD?平面PED,
∴FH∥平面PED,
∵FG∩FH=F,
∴平面FGH∥平面PED;
(Ⅱ)解:∵EA⊥平面ABCD,∴PD⊥平面ABCD,∴PD⊥AD,PD⊥CD.
又∵四边形ABCD是正方形,∴AD⊥CD.
如图建立空间直角坐标系,∵AD=PD=2EA,∴D(0,0,0),P(0,0,2),A(2,0,0),C(0,2,0),B(2,2,0),E(2,0,1).
∵F,G,H分别为PB,EB,PC的中点,∴F(1,1,1),G(2,1,0.5),H(0,1,1).
∴
| GF |
| GH |
设
| n1 |
|
再令y1=1,得
| n1 |
同理可得平面PBC的一个法向量为
| n2 |
∴|cos<
| n1 |
| n2 |
| ||
| 2 |
∴平面FGH与平面PBC所成锐二面角的大小为
| π |
| 4 |
点评:本题考查了线面平行的判定,考查了线线角和面面角,训练了利用平面法向量求解二面角的大小,解答此类问题的关键是正确建系,准确求用到的点的坐标,此题是中档题.

练习册系列答案
相关题目
若α是钝角,则θ=kπ+α,k∈Z是( )
| A、第二象限角 |
| B、第三象限角 |
| C、第二象限角或第三象限角 |
| D、第二象限角或第四象限角 |
一条直线与一个平面垂直的条件是( )
| A、垂直于平面内的一条直线 |
| B、垂直于平面内的两条直线 |
| C、垂直于平面内的无数条直线 |
| D、垂直于平面内的两条相交直线 |
 如图,在平行四边形ABCD中,|AB|=3,|BC|=2,
如图,在平行四边形ABCD中,|AB|=3,|BC|=2,