题目内容
7.已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=-2-\frac{\sqrt{3}t}{2}}\\{y=\frac{1}{2}t}\end{array}\right.$曲线C2的极坐标方程为ρ=2$\sqrt{2}$cos(θ-$\frac{π}{4}$),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.(1)求曲线C2的直角坐标方程;
(2)求曲线C2上的动点M到直线C1的距离的最大值.
分析 (Ⅰ)由ρ2=x2+y2,y=ρsinθ,x=ρcosθ,能求出C2的直角坐标方程.
(Ⅱ)曲线C1消去参数,得C1的直角坐标方程为$x+\sqrt{3}y+2=0$,求出圆心到直线C1的距离,由此能求出动点M到曲线C1的距离的最大值.
解答 解:(Ⅰ)$ρ=2\sqrt{2}cos({θ-\frac{π}{4}})=2({cos{\;}θ+sin{\;}θ})$,…(2分)
即ρ2=2(ρcosθ+ρsinθ),
∴x2+y2-2x-2y=0,
故C2的直角坐标方程为(x-1)2+(y-1)2=2.…(5分)
(Ⅱ)∵曲线C1的参数方程为$\left\{\begin{array}{l}{x=-2-\frac{\sqrt{3}t}{2}}\\{y=\frac{1}{2}t}\end{array}\right.$,
∴C1的直角坐标方程为$x+\sqrt{3}y+2=0$,
由(Ⅰ)知曲线C2是以(1,1)为圆心的圆,
且圆心到直线C1的距离$d=\frac{{\left|{1+\sqrt{3}+2}\right|}}{{\sqrt{{1^2}+{{({\sqrt{3}})}^2}}}}=\frac{{3+\sqrt{3}}}{2}$,…(8分)
∴动点M到曲线C1的距离的最大值为$\frac{{3+\sqrt{3}+2\sqrt{2}}}{2}$.…(10分)
点评 本题考查曲线的直角坐标方程的求法,考查点到曲线的距离的最大值的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.将一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设两条直线l1:ax+by=2与l2:x+2y=2平行的概率为P1,相交的概率为P2,则点P(36P1,36P2)与圆C:x2+y2=1098的位置关系是( )
| A. | 点P在圆C上 | B. | 点P在圆C外 | C. | 点P在圆C内 | D. | 不能确定 |
19.阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )
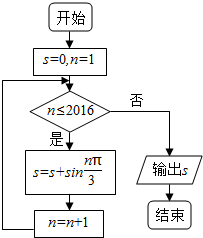

| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $336\sqrt{3}$ |