题目内容
2．已知曲线C的极坐标方程是ρ=2sinθ，直线l的参数方程是$\left\{\begin{array}{l}{x=-\frac{3}{5}t+2}\\{y=\frac{4}{5}t}\end{array}\right.$（t为参数）（Ⅰ）将曲线C的极坐标方程化为直角坐标方程；
（Ⅱ）设直线l与x轴的交点是M，N是曲线C上一动点，求MN的最大值．
分析 （Ⅰ）曲线C的极坐标方程可化为ρ2=2ρsinθ，由此能求出曲线C的直角坐标方程．
（Ⅱ）将直线l的参数方程化为直角坐标方程，求出M点的坐标，从而得到|MC|，再由|MN|≤|MC|+r，能求出MN的最大值．
解答 解：（Ⅰ）曲线C的极坐标方程可化为ρ2=2ρsinθ，…（2分）
又x2+y2=ρ2，x=ρcosθ，y=ρsinθ，
∴曲线C的直角坐标方程为x2+y2-2y=0．…（4分）
（Ⅱ）将直线l的参数方程化为直角坐标方程，得y=-$\frac{4}{3}（x-2）$．…（6分）
令y=0，得x=2，即M点的坐标为（2，0）．
又曲线C为圆，圆C的圆心坐标为C（0，1），半径r=1，
∵直线l与x轴的交点是M，∴M（2，0），
∴|MC|=$\sqrt{4+1}$=$\sqrt{5}$，…（8分）
∵N是曲线C上一动点，∴|MN|≤|MC|+r=$\sqrt{5}+1$．
故MN的最大值为$\sqrt{5}+1$．…（10分）
点评 本题考查曲线的直角坐标方程的求法，考查线段长的最大值的求法，是中档题，解题时要认真审题，注意两点间距离公式的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．已知f（x）=sin（ωx+φ）（ω＞0，|φ|＜π）的图象相邻的对称轴之间的距离为2π，将其向左平移$\frac{π}{2}$个单位，所得函数图象与g（x）=cos（ωx+$\frac{π}{3}$）重合，则φ的值为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{7π}{12}$ | D． | $\frac{2π}{3}$ |
10．已知f（x）对任意x∈[0，+∞）都有f（x+1）=-f（x），且当x∈[0，1）时，f（x）=x，若函数g（x）=f（x）-loga（x+1）（0＜a＜1）在区间[0，4]上有两个零点，则实数a的取值范围是（ ）
| A． | [$\frac{1}{4}$，$\frac{1}{3}$] | B． | [$\frac{1}{4}$，$\frac{1}{3}$） | C． | [$\frac{1}{5}$，$\frac{1}{3}$） | D． | [$\frac{1}{5}$，$\frac{1}{3}$] |
．
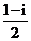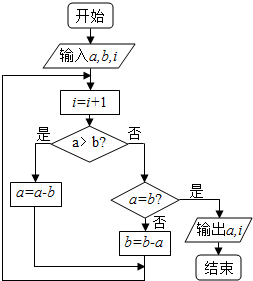如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b，i的值分别为6，8，0，则输出a和i的值分别为（ ）