题目内容
17.设函数f(x)是定义在R上的奇函数,且f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(x+1),x≥0}\\{g(x),x<0}\end{array}\right.$,则g[f(-7)]=( )| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
分析 先设x<0,则-x>0,根据函数的奇偶性,即可求出g(x),再代值计算即可.
解答 解:函数f(x)是定义在R上的奇函数,且f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(x+1),x≥0}\\{g(x),x<0}\end{array}\right.$,
设x<0,则-x>0,则f(-x)=log2(-x+1),
∵f(-x)=-f(x),
∴f(x)=-f(-x)=-log2(-x+1),
∴g(x)=-log2(-x+1)(x<0),
∴f(-7)=g(-7)=-log2(7+1)=-3,
∴g(-3)=-log2(3+1)=-2,
故选:D.
点评 本题考查了函数的奇偶性和函数解析式的求法以及函数值的求法,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
9.已知函数f(x)=Asin(ωx+φ)的图象如图所示,则该函数的解析式可能是( )
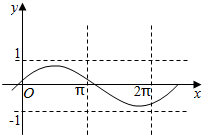

| A. | f(x)=$\frac{3}{4}$sin($\frac{3}{2}$x+$\frac{π}{6}$) | B. | f(x)=$\frac{4}{5}$sin($\frac{4}{5}$x+$\frac{1}{5}$) | C. | f(x)=$\frac{4}{5}$sin($\frac{5}{6}$x+$\frac{π}{6}$) | D. | f(x)=$\frac{4}{5}$sin($\frac{2}{3}$x-$\frac{1}{5}$) |
6.在△ABC中,∠A=60°,AC=2$\sqrt{3}$,BC=3$\sqrt{2}$,则角B等于( )
| A. | 30° | B. | 45° | C. | 90° | D. | 135° |
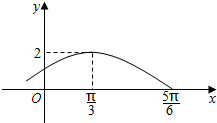 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.