题目内容
16.设Sn为数列{an}的前n项和,已知a1=2,对任意n∈N*,都有2Sn=(n+1)an.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{$\frac{4}{{a}_{n}({a}_{n}+2)}$}的前n项和为Tn,求证:$\frac{1}{2}$≤Tn<1.
分析 (I)2Sn=(n+1)an,当n≥2时,2Sn-1=nan-1,可得$\frac{{a}_{n}}{n}$=$\frac{{a}_{n-1}}{n-1}$=$\frac{{a}_{1}}{1}$,可得an.
(II)$\frac{4}{{a}_{n}({a}_{n}+2)}$=$\frac{4}{2n(2n+2)}$=$\frac{1}{n}-\frac{1}{n+1}$.利用“裂项求和”与数列的单调性即可得出.
解答 (I)解:∵2Sn=(n+1)an,
∴当n≥2时,2Sn-1=nan-1,可得2an=(n+1)an-nan-1,
∴$\frac{{a}_{n}}{n}$=$\frac{{a}_{n-1}}{n-1}$.
∴$\frac{{a}_{n}}{n}$=$\frac{{a}_{1}}{1}$,
∴an=2n.
(II)证明:$\frac{4}{{a}_{n}({a}_{n}+2)}$=$\frac{4}{2n(2n+2)}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴Tn=$(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=1-$\frac{1}{n+1}$.
∴$\frac{1}{2}$=T1≤Tn<1,
∴$\frac{1}{2}$≤Tn<1.
点评 本题考查了递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.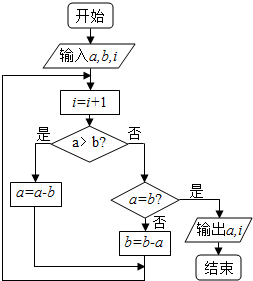 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )| A. | 0,3 | B. | 0,4 | C. | 2,3 | D. | 2,4 |
6.在△ABC中,∠A=60°,AC=2$\sqrt{3}$,BC=3$\sqrt{2}$,则角B等于( )
| A. | 30° | B. | 45° | C. | 90° | D. | 135° |