题目内容
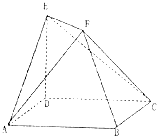 如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD.
如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD.(1)求证:BF⊥AC:
(2)求几何体ABCDEF的体积.
考点:棱柱、棱锥、棱台的体积
专题:证明题,空间位置关系与距离
分析:(1)运用线面垂直的判定和性质,即可得证;
(2)将多面体分割成棱锥A-BDEF和C-BDEF,则VABCDEF=VA-BDEF+VC-BDEF=2VA-BDEF,运用三棱锥的条件公式即可得到体积.
(2)将多面体分割成棱锥A-BDEF和C-BDEF,则VABCDEF=VA-BDEF+VC-BDEF=2VA-BDEF,运用三棱锥的条件公式即可得到体积.
解答:
(1)证明:∵四边形ABCD为正方形,
∴AC⊥BD,又ED⊥平面ABCD
∴ED⊥AC 而ED∩BD=D
∴AC⊥平面EFBD;
又BF?平面EFBD,
∴AC⊥BF.
(2)解:VABCDEF=VA-BDEF+VC-BDEF=2VA-BDEF
又BD=4
,EF=2
V=
×
(4
+2
)×2×2
×2=16.

∴AC⊥BD,又ED⊥平面ABCD
∴ED⊥AC 而ED∩BD=D
∴AC⊥平面EFBD;
又BF?平面EFBD,
∴AC⊥BF.
(2)解:VABCDEF=VA-BDEF+VC-BDEF=2VA-BDEF
又BD=4
| 2 |
| 2 |
V=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查线面垂直的判定和性质,同时考查割补思想,以及棱锥的体积公式.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
若存在过点(1,1)的直线与曲线y=x2+x和y=ax2-x-1都相切,则a等于( )
| A、-1或-3 | B、-2或3 |
| C、-1或3 | D、1或-3 |
已知函数f(x)=|x+a|(a∈R)在[-1,1]上的最大值为M(a),则函数g(x)=M(x)-|x2-1|的零点的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知全集U={1,2,3,4,5,6},集合M={2,3,5},N={4,5},则∁U(M∪N)的元素个数有( )
| A、0个 | B、1个 | C、2 | D、3个 |
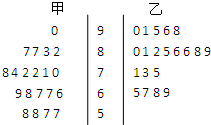 为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.