题目内容
某镇人口第二年比第一年增长m%,第三年比第二年增长n%,又这两年的平均增长率为p%,则p与
的关系为( )
| m+n |
| 2 |
A、p>
| ||
B、p=
| ||
C、p≤
| ||
D、p≥
|
考点:不等式比较大小
专题:等差数列与等比数列
分析:先根据题意列出方程,再由基本不等式可得出出p%和
的大小关系
| m%+n% |
| 2 |
解答:
解:由题意知:(1+p%)2=(1+m%)(1+n%),
∴1+p%=
≤
=1+
,
∴p%≤
,即p≤
,当且仅当m=n时等号成立,
故选:C.
∴1+p%=
| (1+m%)(1+n%) |
| (1+m%)+(1+n%) |
| 2 |
| m%+n% |
| 2 |
∴p%≤
| m%+n% |
| 2 |
| m+n |
| 2 |
故选:C.
点评:本题考查基本不等式在实际生活中的应用,不等式大小的比较,根据题意列出关系式是解决问题的关键,属基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
函数f(x)=lg
的定义域为( )
| x2-9 |
| A、[3,+∞) |
| B、(3,+∞) |
| C、(-∞,-3]∪[3,+∞) |
| D、(-∞,-3)∪(3,+∞) |
运行如图所示的流程图,则输出的结果S是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)的图象如图所示,下列数值排序正确的是( )
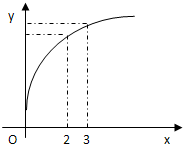

| A、0<f′(3)<f(3)-f(2)<f′(2) |
| B、0<f′(2)<f′(3)<f(3)-f(2) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-f(2)<f′(2)<f′(3) |
若方程4x+(m-3)•2x+m=0有两个不相同的实根,则实数m的取值范围是( )
| A、m>0 | B、m>1 |
| C、0≤m≤1 | D、0<m<1 |
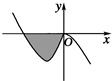 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为