题目内容
已知函数f(x)=
,x≥1.
(1)当a=1时,求f(x)的最大值;
(2)对任意x≥1,f(x)>0恒成立,求实数a的取值范围.
| x |
| x2+ax+2 |
(1)当a=1时,求f(x)的最大值;
(2)对任意x≥1,f(x)>0恒成立,求实数a的取值范围.
考点:函数的最值及其几何意义
专题:综合题,不等式的解法及应用
分析:(1)当a=1时,f(x)=
=
,利用基本不等式求f(x)的最大值;
(2)对任意x≥1,f(x)>0恒成立,对任意x≥1,x2+ax+2>0恒成立,可得a>-(x+
),利用基本不等式求的最值,即可求实数a的取值范围.
| x |
| x2+x+2 |
| 1 | ||
x+
|
(2)对任意x≥1,f(x)>0恒成立,对任意x≥1,x2+ax+2>0恒成立,可得a>-(x+
| 2 |
| x |
解答:
解:(1)当a=1时,f(x)=
=
,
∵x≥1,
∴x+
≥2
,
∴f(x)≤
=
;
(2)对任意x≥1,f(x)>0恒成立,
∴对任意x≥1,x2+ax+2>0恒成立,
∴a>-(x+
),
∵x+
≥2
,
∴-(x+
)≤-2
,
∴a>-2
.
| x |
| x2+x+2 |
| 1 | ||
x+
|
∵x≥1,
∴x+
| 2 |
| x |
| 2 |
∴f(x)≤
| 1 | ||
2
|
2
| ||
| 7 |
(2)对任意x≥1,f(x)>0恒成立,
∴对任意x≥1,x2+ax+2>0恒成立,
∴a>-(x+
| 2 |
| x |
∵x+
| 2 |
| x |
| 2 |
∴-(x+
| 2 |
| x |
| 2 |
∴a>-2
| 2 |
点评:本题考查函数的最值及其几何意义,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
某镇人口第二年比第一年增长m%,第三年比第二年增长n%,又这两年的平均增长率为p%,则p与
的关系为( )
| m+n |
| 2 |
A、p>
| ||
B、p=
| ||
C、p≤
| ||
D、p≥
|
方程x=2+log
x的根所在的区间是( )
| 1 |
| 2 |
| A、(1,2) |
| B、(0,1) |
| C、(2,3) |
| D、(4,5) |
将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:
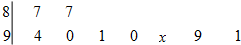
则7个剩余分数的方差为( )
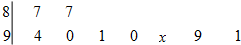
则7个剩余分数的方差为( )
A、
| ||||
B、
| ||||
| C、36 | ||||
D、
|
判断方程(
)x=x2的根的个数是( )
| 1 |
| 2 |
| A、4个 | B、3个 | C、2个 | D、1个 |