题目内容
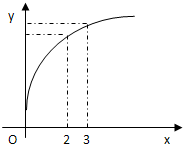
函数f（x）的图象如图所示，下列数值排序正确的是（ ）
| A、0＜f′（3）＜f（3）-f（2）＜f′（2） |
| B、0＜f′（2）＜f′（3）＜f（3）-f（2） |
| C、0＜f′（3）＜f′（2）＜f（3）-f（2） |
| D、0＜f（3）-f（2）＜f′（2）＜f′（3） |
考点：利用导数研究函数的单调性
专题：
分析：观察图象及导数的几何意义得：0＜f′(3)＜
＜f′(2)，即函数在（2，3）上增长得越来越慢，所以导数值为正，且绝对值越来越小，故f′（2）＞f′（3），同时根据割线的性质，一定可以在（2，3）之间找到一点其切线的斜率等于割线斜率，即其导数值等于割线的斜率，由此可得结论．
| f(3)-f(2) |
| 3-2 |
解答：
解：观察图象可知，该函数在（2，3）上为连续可导的增函数，且增长的越来越慢．
所以各点处的导数在（2，3）上处处为正，且逐渐减小，所以故f′（2）＞f′（3），
而f（3）-f（2）=
，表示的连接点（2，f（2））与点（3，f（3））割线的斜率，根据导数的几何意义，一定可以在（2，3）之间找到一点，该点处的切线与割线平行，则割线的斜率就是该点处的切线的斜率，即该点处的导数，则根据刚才的分析，必有：0＜f′(3)＜
＜f′(2)．
故选A．
所以各点处的导数在（2，3）上处处为正，且逐渐减小，所以故f′（2）＞f′（3），
而f（3）-f（2）=
| f(3)-f(2) |
| 3-2 |
| f(3)-f(2) |
| 3-2 |
故选A．
点评：本题考查了函数的导数与函数单调性的关系，以及割线与切线间的关系，要注意数形结合来解题．
练习册系列答案
相关题目
已知函数y=x2+（b+1）x+c在（-∞，1）是单调递减函数，则b取值范围是（ ）
| A、b≥-3 | B、b≤-3 |
| C、b＞-3 | D、b＜-3 |
已知集合A={1，2，3}，B={2，3，4}，则A∪B=（ ）
| A、{2，3} |
| B、{1，4} |
| C、{1，2，3，4} |
| D、{1，3，4} |
某镇人口第二年比第一年增长m%，第三年比第二年增长n%，又这两年的平均增长率为p%，则p与
的关系为（ ）
| m+n |
| 2 |
A、p＞
| ||
B、p=
| ||
C、p≤
| ||
D、p≥
|
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图．则这10天甲加工零件的平均数及乙加工零件的中位数分别为（ ）| A、23，24 |
| B、24，24 |
| C、24，23 |
| D、23，23 |