题目内容
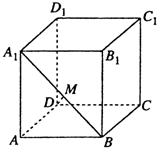 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.(Ⅰ)若E为棱DD1上的点,试确定点E的位置,使平面A1C1E∥B1D;
(Ⅱ)若M为A1B上的一动点,求证:DM∥平面D1B1C.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)当E为棱DD1上的中点时,平面A1C1E∥B1D;连接A1C1,与D1B1相交于O,连接OE,得到OE∥B1D,根据线面平行的判定定理可证;
(Ⅱ)连接A1D,BD,只要证明平面A1BD∥平面D1B1C.再由面面平行的性质可得所证.
(Ⅱ)连接A1D,BD,只要证明平面A1BD∥平面D1B1C.再由面面平行的性质可得所证.
解答:
解:(Ⅰ)当E为棱DD1上的中点时,平面A1C1E∥B1D;如图,

连接A1C1,与D1B1相交于O,E为DD1上的中点,连接OE,得到OE∥B1D,
OE?平面A1C1E,B1D,?平面 A1C1E,
∴B1D∥平面A1C1E;
(Ⅱ)连接A1D,BD,因为几何体为正方体,如图,
所以A1D∥B1C,A1B∥D1C,
所以平面A1BD∥平面D1B1C.
DM?∥平面DA1BD.
所以DM∥平面D1B1C.

连接A1C1,与D1B1相交于O,E为DD1上的中点,连接OE,得到OE∥B1D,
OE?平面A1C1E,B1D,?平面 A1C1E,
∴B1D∥平面A1C1E;
(Ⅱ)连接A1D,BD,因为几何体为正方体,如图,
所以A1D∥B1C,A1B∥D1C,
所以平面A1BD∥平面D1B1C.
DM?∥平面DA1BD.
所以DM∥平面D1B1C.
点评:本题考查了正方体为载体的空间线面平行的判定,关键是将线面平行转化为线线平行解答.

练习册系列答案
相关题目
下列函数中,在(0,+∞)既是增函数又是奇函数的是( )
| A、y=x+1 | ||
B、y=x+
| ||
C、y=x-
| ||
| D、y=x2+1 |
设四个点P、A、B、C在同一球面上,且PA、PB、PC两两垂直,PA=3,PB=4,PC=5,那么这个球的表面积是( )
A、20
| ||
B、25
| ||
| C、25π | ||
| D、50π |
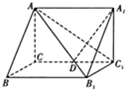 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,D是棱CC1的中点,A1D⊥AB1;
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,D是棱CC1的中点,A1D⊥AB1;