题目内容
等差数列{an}的前n项和为Sn,若a10+a12=2,则S21的值是 .
考点:等差数列的前n项和,其他不等式的解法
专题:等差数列与等比数列
分析:由等差数列的性质结合a10+a12=2求得a11,再由等差数列的前n项和得答案.
解答:
解:在等差数列{an}中,由a10+a12=2,得
2a11=2,则a11=1,
∴S21=21a11=21×1=21.
故答案为:21.
2a11=2,则a11=1,
∴S21=21a11=21×1=21.
故答案为:21.
点评:本题考查了等差数列的性质,考查了等差数列的前n项和,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于函数y=-
的单调性的叙述正确的是( )
| 3 |
| x |
| A、在(-∞,0)上是递增的,在(0,+∞)上是递减的 |
| B、在(-∞,0)∪(0,+∞)上是递增的 |
| C、在[0,+∞)上递增 |
| D、在(-∞,0)和(0,+∞)上都是递增的 |
已知函数f(x)=
,若f(x)≥ax恒成立,则a的取值范围是( )
|
A、(∞,
| ||||
B、[-
| ||||
C、[
| ||||
| D、[1,+∞) |
下列说法正确的是( )
| A、命题“?x∈R,ex>0”的否定是“?x∈R,ex<0” |
| B、命题“已知x,y∈R,若x+y≠10”,则x≠5或y≠5是真命题 |
| C、x2+2x≥ax在x∈[0,2]上恒成立?(x2+2x)min≥(ax)min在x∈[0,2]上恒成立” |
| D、命题:若a=-1,则函数f(x)=ax2+2x-1只有一个零点的逆命题为真命题 |
函数y=x2-4x+2,x∈[1,3]的最小值为( )
| A、0 | B、-1 | C、-2 | D、3 |
 如图OPQ是半径为
如图OPQ是半径为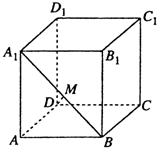 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.