题目内容
如图,点P为⊙O的弦AB上一点,且AP=16,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为 .


考点:与圆有关的比例线段
专题:立体几何
分析:由已知得PC2=AP•PB=16×4=64,由此能求出PC的长.
解答:
解:∵点P为⊙O的弦AB上一点,且AP=16,BP=4,
连接OP,作PC⊥OP交圆于C,
∴PC2=AP•PB=16×4=64,
∴PC=8.
故答案为:8.
连接OP,作PC⊥OP交圆于C,
∴PC2=AP•PB=16×4=64,
∴PC=8.
故答案为:8.
点评:本题考查线段长的求法,是中档题,解题时要认真审题,注意相交弦定理的合理运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知椭圆E:
+
=1(a>b>0)的左焦点为F(-2,0)过点F的直线交椭圆于A,B两点.若AB的中点坐标为(-1,
),则E的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
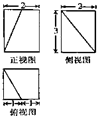

| A、9 | ||
| B、10 | ||
| C、11 | ||
D、
|
下列说法正确的是( )
| A、命题“?x∈R,ex>0”的否定是“?x∈R,ex<0” |
| B、命题“已知x,y∈R,若x+y≠10”,则x≠5或y≠5是真命题 |
| C、x2+2x≥ax在x∈[0,2]上恒成立?(x2+2x)min≥(ax)min在x∈[0,2]上恒成立” |
| D、命题:若a=-1,则函数f(x)=ax2+2x-1只有一个零点的逆命题为真命题 |
在△ABC中,三边a,b,c与面积S的关系是S=
,则∠C=( )
| a2+b2-c2 |
| 4 |
| A、30° | B、60° |
| C、45° | D、90° |
设集合A={(x,y)|
},则A=( )
|
A、
| |||||
| B、(3,-3) | |||||
| C、{(3,-3)} | |||||
| D、x=3,y=-3 |
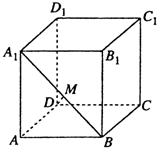 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.