题目内容
已知线段OA,OB,OC两两垂直,且OA=1,OB=1,OC=2.若线段OA,OB,OC在直线OP上的射影长相等,则其射影长为 .
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离,空间角
分析:首先利用勾股定理求出解得:AC=BC=
,AB=
,利用余弦定理:AB2=AC2+BC2-2AC•BCcos∠ACB解得:cos∠ACB=
进一步求得:sin∠ACB=
,再求出S△ABC=
•
•
sin∠ACB=
最后利用:利用三棱锥的体积相等,VC-AOB=VO-ABC解得高,即射影的长.
| 5 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
| 3 |
| 2 |
解答:
解:线段OA,OB,OC两两垂直,且OA=1,OB=1,OC=2.若线段OA,OB,OC在直线OP上的射影长相等.
解得:AC=BC=
,AB=
利用余弦定理:
AB2=AC2+BC2-2AC•BCcos∠ACB
解得:cos∠ACB=
则:sin∠ACB=
S△ABC=
•
•
sin∠ACB=
利用三棱锥的体积相等
VC-AOB=VO-ABC
•
•1•1•2=
•
h
解得:h=
故答案为:
解得:AC=BC=
| 5 |
| 2 |
利用余弦定理:
AB2=AC2+BC2-2AC•BCcos∠ACB
解得:cos∠ACB=
| 4 |
| 5 |
则:sin∠ACB=
| 3 |
| 5 |
S△ABC=
| 1 |
| 2 |
| 5 |
| 5 |
| 3 |
| 2 |
利用三棱锥的体积相等
VC-AOB=VO-ABC
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
解得:h=
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查的知识要点:线面的夹角,直线在平面上的射影,余弦定理的应用,三角形的面积及相关的运算问题,属于中等题型.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
关于函数y=-
的单调性的叙述正确的是( )
| 3 |
| x |
| A、在(-∞,0)上是递增的,在(0,+∞)上是递减的 |
| B、在(-∞,0)∪(0,+∞)上是递增的 |
| C、在[0,+∞)上递增 |
| D、在(-∞,0)和(0,+∞)上都是递增的 |
已知椭圆E:
+
=1(a>b>0)的左焦点为F(-2,0)过点F的直线交椭圆于A,B两点.若AB的中点坐标为(-1,
),则E的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
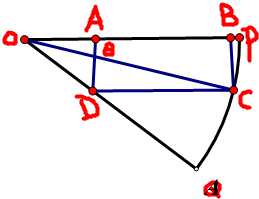 如图OPQ是半径为
如图OPQ是半径为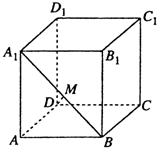 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.